设数列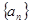 的前
的前 项和为
项和为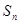 ,且满足
,且满足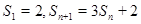
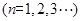 .
.
(Ⅰ)求证:数列 为等比数列;
为等比数列;
(Ⅱ)求通项公式 ;
;
(Ⅲ)若数列 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列 的前
的前 项和为
项和为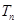 .
.
已知函数f(x)= ,(x>0,
,(x>0,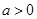 ).
).
(1) 当a=4时,求函数f(x)的最小值;
(2) 若函数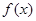 >-x+4,求实数
>-x+4,求实数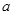 的取值范围
的取值范围
已知函数f(x)=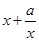 ,x∈
,x∈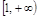 ,
,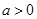 .
.
(1) 当a= 时,求函数f(x)的最小值;
时,求函数f(x)的最小值;
(2) 若函数 的最小值为4,求实数
的最小值为4,求实数
设数列{ }是等差数列,数列{
}是等差数列,数列{ }的前
}的前 项和
项和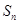 满足
满足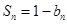 ,
, ,
,
且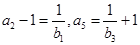 。
。
(1)求数列{ }和{
}和{ }的通项公式:
}的通项公式:
(2)设 为数列{
为数列{ .
. }的前
}的前 项和,求
项和,求 .
.
某企业生产A,B两种产品,生产每吨产品所需的劳动力和煤、电耗如下表: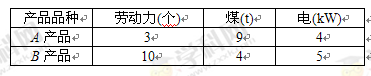
已知生产每吨A产品的利润是5万元,生产每吨B产品的利润是10万元,现因条件限制,该企业仅有劳动力300个,煤360 t,并且供电局只能供电200 kW,试问该企业生产A,B两种产品各多少吨,才能获得最大利润?
火车站 北偏东
北偏东 方向的
方向的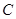 处有一电视塔,火车站正东方向的
处有一电视塔,火车站正东方向的 处有一小汽车,测得
处有一小汽车,测得 距离为31
距离为31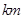 ,该小汽车从
,该小汽车从 处以60公里每小时的速度前往火车站,20分钟后到达
处以60公里每小时的速度前往火车站,20分钟后到达 处,测得离电视塔21
处,测得离电视塔21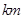 ,问小汽车到火车站还需多长时间?
,问小汽车到火车站还需多长时间?