招聘会上,某公司决定先试用后再聘用小强,该公司的甲、乙两个部门各有4个不同岗位.
(Ⅰ)公司随机安排小强在这两个部门中的3个岗位上进行试用,求小强试用的3个岗位中恰有2个在甲部门的概率;
(Ⅱ)经试用,甲、乙两个部门都愿意聘用他.据估计,小强可能获得的岗位月工资及相应概率如下表所示:
甲部门不同岗位月工资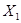 (元) (元) |
2200 |
2400 |
2600 |
2800 |
获得相应岗位的概率 |
0.4 |
0.3 |
0.2 |
0.1 |
乙部门不同岗位月工资 (元) (元) |
2000 |
2400 |
2800 |
3200 |
获得相应岗位的概率 |
0.4 |
0.3 |
0.2 |
0.1 |
求甲、乙两部门月岗位工资的期望与方差,据此请帮助小强选择一个部门,并说明理由.
如图,已知椭圆C的方程为 ,双曲线
,双曲线 的两条渐近线为
的两条渐近线为 ,过椭圆C的右焦点F作直线
,过椭圆C的右焦点F作直线 ,使
,使 交于点P,设
交于点P,设 与椭圆C的两个焦点由上至下依次为A,B.
与椭圆C的两个焦点由上至下依次为A,B.
(1)若 的夹角为60,且双曲线的焦距为4,求椭圆C的方程;
的夹角为60,且双曲线的焦距为4,求椭圆C的方程;
(2)若 ,求椭圆C的离心率.
,求椭圆C的离心率.
已知正 的边长为4,CD是AB边上的高,E,F分别是AC和BC边上的中点,现将
的边长为4,CD是AB边上的高,E,F分别是AC和BC边上的中点,现将 沿CD翻折成直二面角A-BC-B.
沿CD翻折成直二面角A-BC-B.
(1)求二面角E-DF-C的余弦值;
(2)在线段BC上是否存在一点P,使AP DE?如果存在,求出
DE?如果存在,求出 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
某省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布 现从该省某校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组[157.5,162.5]第二组[162.5,167.5],...第6组[182.5,187.5],下图是按上述分组方法得到的频率分布直方图.
现从该省某校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组[157.5,162.5]第二组[162.5,167.5],...第6组[182.5,187.5],下图是按上述分组方法得到的频率分布直方图.
(1)求该学校高三年级男生的平均身高;
(2)求这50名男生身高在177.5cm以上(含177.5cm)的人数;
(3)在这50名男生身高在177.5cm以上含(177.5cm)的人中任意抽取2人,该2人中身高排名(从高
到低)在全省前130名的人数记为 ,求
,求 的数学期望.
的数学期望.
参考数据:若 ~
~ .则
.则 ,
, ,
, .
.
已知数列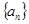 的前
的前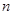 项和
项和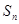 与通项
与通项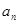 满足
满足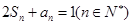 .
.
(1)求数列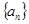 的通项公式;
的通项公式;
(2)数列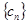 满足
满足 ,求证:
,求证: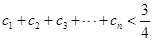 .
.
设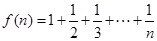 ,是否存在关于自然数n的函数
,是否存在关于自然数n的函数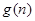 ,使等式
,使等式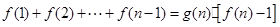 对于
对于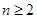 的一切自然数都成立?并证明你的结论.
的一切自然数都成立?并证明你的结论.