(本小题满分13分)
已知抛物线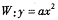 经过点A(2,1),过A作倾斜角互补的两条不同直线
经过点A(2,1),过A作倾斜角互补的两条不同直线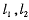 .
.
(1) 求抛物线W的 方程及准线方程;
方程及准线方程;
(2) 当直线 与抛物线W相切时,求直线
与抛物线W相切时,求直线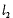 的方程;
的方程;
(3) 设直线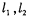 分别交抛物线W于B、C两点(均不与4重合),若以线段BC为直径的圆与抛物线的准线相切,求直线BC的方程.
分别交抛物线W于B、C两点(均不与4重合),若以线段BC为直径的圆与抛物线的准线相切,求直线BC的方程.
已知函数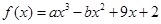 ,若f(x)在x=1处的切线方程为3x+y-6=0
,若f(x)在x=1处的切线方程为3x+y-6=0
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若对任意的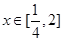 ,都有f(x)
,都有f(x) 成立,求函数g(t)
成立,求函数g(t)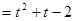 的最值
的最值
已知a为实数, 。
。
⑴求导数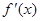 ;
;
⑵若 ,求
,求 在[-2,2] 上的最大值和最小值;
在[-2,2] 上的最大值和最小值;
⑶若 在(-∞,-2)和(2,+∞)上都是递增的,求a的取值范围。
在(-∞,-2)和(2,+∞)上都是递增的,求a的取值范围。
某校的研究性学习小组为了研究高中学生的身体发育状况,在该校随机抽出120名17至18周岁的男生,其中偏重的有60人,不偏重的也有60人。在偏重的60人中偏高的有40人,不偏高的有20人;在不偏重的60人中偏高和不偏高人数各占一半
(1)根据以上数据建立一个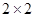 列联表:
列联表:
| 偏重 |
不偏重 |
合计 |
|
| 偏高 |
|||
| 不偏高 |
|||
| 合计 |
(2)请问该校17至18周岁的男生身高与体重是否有关?
已知函数 .
.
(1)求曲线 在点
在点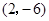 处的切线方程;
处的切线方程;
(2)直线 为曲线
为曲线 的切线,且经过原点,求直线
的切线,且经过原点,求直线 的方程及切点坐标.
的方程及切点坐标.
函数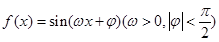 ,在同一个周期内,当
,在同一个周期内,当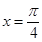 时
时 取最大值1,当
取最大值1,当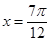 时,
时, 取最小值-1
取最小值-1
(1)求函数的解析式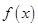 ;
;
(2)若函数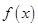 满足方程
满足方程 ;求在
;求在 内的所有实数根之和.
内的所有实数根之和.