 经过点
经过点 ,
, ,
, 经过点
经过点 ,
, ,当直线
,当直线 与
与 平行或垂直时,求
平行或垂直时,求 的值.
的值.
选修4-4:坐标系与参数方程
已知在直角坐标系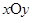 中,以坐标原点为极点,
中,以坐标原点为极点,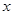 轴正半轴为极轴建立极坐标系,圆锥曲线
轴正半轴为极轴建立极坐标系,圆锥曲线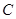 的极坐标方程为
的极坐标方程为
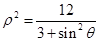 ,定点
,定点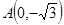 ,
,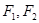 是圆锥曲线
是圆锥曲线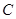 的左、右焦点.
的左、右焦点.
(Ⅰ)求经过点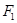 且平行于直线
且平行于直线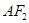 的直线
的直线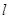 的极坐标方程;
的极坐标方程;
(Ⅱ)设(Ⅰ)中直线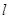 与圆锥曲线
与圆锥曲线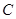 交于
交于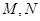 两点,求
两点,求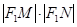 .
.
选修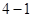 :几何证明选讲
:几何证明选讲
如图,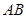 为圆
为圆 直径,且
直径,且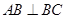 ,圆
,圆 交
交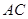 于点
于点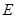 ,过圆心
,过圆心 作
作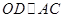 ,交
,交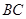 边于
边于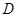 ,交圆
,交圆 于
于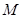 .
.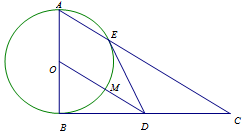
(Ⅰ)求证: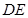 是圆
是圆 的切线;
的切线;
(Ⅱ)求证: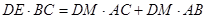 .
.
(本小题满分12分)已知函数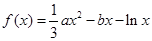 ,其中
,其中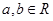 .
.
(Ⅰ)若函数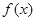 在
在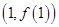 处的切线斜率为
处的切线斜率为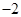 ,在
,在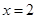 取得极值点,求函数
取得极值点,求函数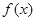 的解析式;
的解析式;
(Ⅱ)当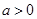 ,且
,且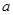 为常数时,若函数
为常数时,若函数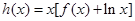 对任意的
对任意的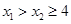 ,总有
,总有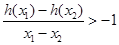 成立,试用
成立,试用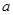 表示出
表示出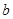 的取值范围.
的取值范围.
(本小题满分12分)已知椭圆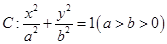 ,点
,点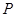 在椭圆
在椭圆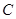 上,且
上,且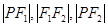 构成等差数列,右焦点
构成等差数列,右焦点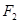 到直线
到直线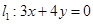 的距离为
的距离为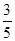 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过椭圆右焦点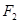 斜率为
斜率为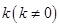 的直线
的直线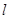 与椭圆C相交于E、F两点,A为椭圆的右顶点,直线AE,AF分别交直线
与椭圆C相交于E、F两点,A为椭圆的右顶点,直线AE,AF分别交直线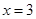 于点M,N,线段MN的中点为P,记直线
于点M,N,线段MN的中点为P,记直线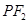 的斜率为
的斜率为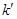 ,求证:
,求证: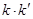 为定值.
为定值.
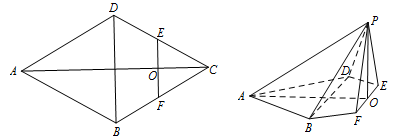
(本小题满分12分)如图,在菱形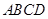 中,
中, ,
,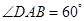 ,
, 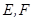 分别是边
分别是边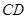 ,
,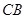 的中点,
的中点,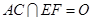 ,沿
,沿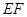 将△
将△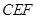 翻折到△
翻折到△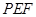 ,连接
,连接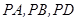 ,得到如图的五棱锥
,得到如图的五棱锥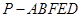 .
.
(Ⅰ)求证: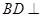 平面
平面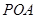 ;
;
(Ⅱ)若 ,求二面角
,求二面角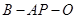 的大小.
的大小.