设数列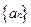 的前n项和为
的前n项和为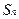 ,且
,且 ,其中p是不为零的常数.
,其中p是不为零的常数.
(1)证明:数列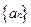 是等比数列;
是等比数列;
(2)当p=3时,若数列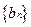 满足
满足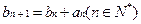 ,
,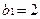 ,求数列
,求数列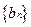 的通项公式.
的通项公式.
已知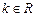 ,函数
,函数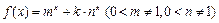 .
.
(1) 如果实数 满足
满足 ,函数
,函数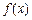 是否具有奇偶性?如果有,求出相应的
是否具有奇偶性?如果有,求出相应的
值,如果没有,说明为什么?
(2) 如果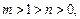 判断函数
判断函数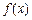 的单调性;
的单调性;
(3) 如果 ,
,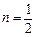 ,且
,且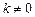 ,求函数
,求函数 的对称轴或对称中心.
的对称轴或对称中心.
如图,直角三角形ABC中,∠B= ,AB=1,B
,AB=1,B C=
C=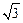 .点M,N分别在边AB和AC
.点M,N分别在边AB和AC
上(M点和B点不重合),将△AMN沿MN翻折,△AMN变为△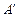 MN,使顶点
MN,使顶点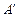 落
落
在边BC上(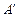 点和B点不重合).设∠AMN=
点和B点不重合).设∠AMN=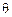 .
.
(1) 用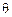 表示线段
表示线段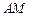 的长度,并写出
的长度,并写出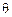 的取值范围;
的取值范围;
(2) 求线段 长度的最小值.
长度的最小值.
已知椭圆的中心为坐标原点,短轴长为2,一条准线方程为l: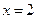 .
.
⑴ 求椭圆的标准方程;
⑵ 设O为坐标原点,F是椭圆的右焦点,点M是直线l上的动点,过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值.

甲打靶射击,有4发子弹,其中有一发是空弹.
(1)求空弹出现在第一枪的概率;
(2)求空弹出现在前三枪的概率;
(3)如果把空弹换成实弹,甲前三枪在靶上留下三个两两距离分别为3,4,5的弹孔 ,第四枪瞄准了三角形
,第四枪瞄准了三角形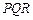 射击,第四个弹孔落在三角形
射击,第四个弹孔落在三角形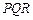 内
内 ,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小).
,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小).