要在一规划区域内建工厂，试画出该工厂由拆迁、设计、购买设备、厂房建设、设备安装到试生产的工序流程图（各工序名称、工序代号、紧前工序入图）.
（注：紧前工序，即为该工序相衔接的前一工序）.
| 工序代号 |
工序名称 |
紧前工序 |
| A |
拆迁 |
—— |
| B |
工程设计 |
—— |
| C |
土建设计 |
B |
| D |
设备采购 |
B |
| E |
厂房土建 |
A，C |
| F |
设备安装 |
D，E |
| G |
设备调试 |
F |
| H |
试生产 |
G |
如图已知：菱形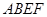
所在平面与直角梯形ABCD所在平面互相垂直，
，
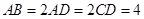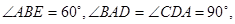点
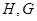分别是线段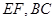
的中点.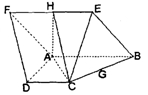
(1)求证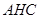：平面
平面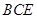
;
(2)试问在线段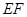
上是否存在点
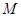，使得
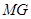
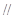平面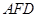
,若存在,求
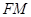的长并证明；若不存在，说明理由.
右表是一个由正数组成的数表，数表中各行依次成等差数列，各列依次成等比数列，且公比都相等，已知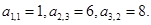
（1）求数列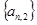
的通项公式；
（2）设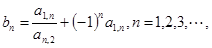
求数列
的前
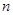项和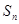
。
已知向量
，
当
时，求函数
的值域：
(2)锐角
中，
分别为角
的对边，若
，求边
.
南昌市为增强市民的交通安全意识，面向全市征召“小红帽”志愿者在部分交通路口协助交警维持交通，把符合条件的1000名志愿者按年龄分组：第1组
、第2组
、第3组
、第4组
、第5组
，得到的频率分布直方图如图所示：
(1)若从第3、4、5组中用分层抽样的方法抽取12名志愿者在五一节这天到广场协助交警维持交通，应从第3、4、5组各抽取多少名志愿者？
(2)在(1)的条件下，南昌市决定在这12名志愿者中在第四或第五组的志愿者中，随机抽取3名志愿者到学校宣讲交通安全知识，求到学校宣讲交通知识的资源者中恰好1名市第五组的概率.
已知函数
若函数
在
和
上是增函数，在
是减函数，求
的值；
讨论函数
的单调递减区间；
如果存在
，使函数
，
，在
处取得最小值，试求
的最大值.