判断如下图所示的几何体是不是棱锥,为什么? 
(本小题满分14分)
如图,三棱柱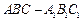 中,侧面
中,侧面
 底面
底面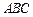 ,
, ,
,
且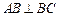 ,O为
,O为 中点.
中点.
(Ⅰ)证明: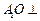 平面
平面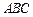 ;
;
(Ⅱ)求直线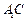 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在 上是否存在一点
上是否存在一点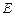 ,使得
,使得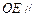 平面
平面 ,若不存在,说明理由;若存在,
,若不存在,说明理由;若存在,
确定点 的位置.
的位置.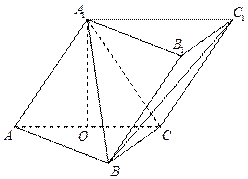
(本小题满分14分)
某人上楼梯,每步上一阶的概率为,每步上二阶的概率,设该人从台阶下的平台开始出发,到达第n阶的概率为Pn.
(I)求P2;
(II)该人共走了5,求该人这5步共上的阶数x的数学期望.
(本小题满分14分)
已知A、B是直线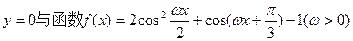 图像的两个相邻交点,且
图像的两个相邻交点,且
(I)求 的值;
的值;
(II)在锐角 中,a,b,c分别是角A,B,C的对边,若
中,a,b,c分别是角A,B,C的对边,若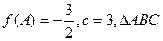
的面积为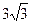 ,求a的值.
,求a的值.
若由数列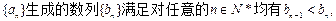
 “Z数列”
“Z数列”
(1)在数列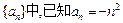 ,试判断数列
,试判断数列 是否为“Z数列”;
是否为“Z数列”;
(2)若数列 是“Z数列”,
是“Z数列”, ;
;
(3)若数列 是“Z数列”,设
是“Z数列”,设 。
。
已知抛物线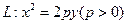 和点M(2,2),若抛物线L上存在不同的两点A、B满足
和点M(2,2),若抛物线L上存在不同的两点A、B满足 。
。
(1)求实数p的取值范围;
(2)当 时,抛物线L上是否存在异于A、B的点C,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线?若存在,求出点C的坐标;若不存在,请说明理由。
时,抛物线L上是否存在异于A、B的点C,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线?若存在,求出点C的坐标;若不存在,请说明理由。