已知抛物线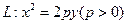 和点M(2,2),若抛物线L上存在不同的两点A、B满足
和点M(2,2),若抛物线L上存在不同的两点A、B满足 。
。
(1)求实数p的取值范围;
(2)当 时,抛物线L上是否存在异于A、B的点C,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线?若存在,求出点C的坐标;若不存在,请说明理由。
时,抛物线L上是否存在异于A、B的点C,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线?若存在,求出点C的坐标;若不存在,请说明理由。
中,角
所对的边分别为
,已知
,
,
,
(1)求
的值;
(2)求
的面积.
海关对同时从 三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如右表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测
三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如右表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测
| 地区 |
 |
 |
 |
| 数量 |
50 |
150 |
100 |
(1)求这6件样品中来自 各地区商品的数量;
各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进一步检测,求这2件商品来自相同地区的概率.
将连续正整数
从小到大排列构成一个数
,
为这个数的位数(如
时,此数为 ,共有15个数字,
),现从这个数中随机取一个数字,
为恰好取到0的概率.
,共有15个数字,
),现从这个数中随机取一个数字,
为恰好取到0的概率.
(1)求
;
(2)当
时,求
的表达式;
(3)令
为这个数中数字0的个数,
为这个数中数字9的个数,
,
,求当
,时
的最大值.
如图,已知抛物线
,过点
任作一直线与
相交于
两点,过点
作
轴的平行线与直线
相交于点
(
为坐标原点).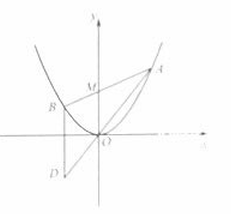
(1)证明:动点
在定直线上;
(2)作
的任意一条切线
(不含
轴)与直线
相交于点
,与(1)中的定直线相交于点
,证明:
为定值,并求此定值.
如图,三棱柱
中,
,
(1)求证:
;
(2)若
,问
为何值时,三棱柱
体积最大,并求此最大值.