如图所示，小明设计了某个产品的包装盒，他少设计了其中一部分，请你把它补上，使其成为两边均有盖的正方体盒子． 
(1)你有__________种弥补的办法.
(2)任意画出一种成功的设计图．
（本小题满分14分）矩形纸片ABCD的边AB=6，AD=10，点E、F分别在边AB和BC上（不含端点）. 现将纸片的右下角沿EF翻折，使得顶点B翻折后的新位置B1恰好落在边AD上. 设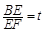
，EF=l，l关于t的函数为
. 
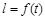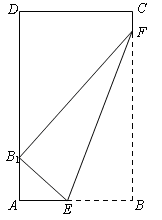
试求：（1）函数f(t)的定义域；
（2）函数f(t)的最小值.
如图，将圆分成n个区域，用3种不同颜色给每一个区域染色，要求相邻区域颜色互异，把不同的染色方法种数记为
。求
（1）
及与
的关系式；
（2）数列
的通项公式，并证明：
如图，正四棱锥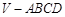
的底面边长为2a，高为h. 以其底面中心O为坐标原点建立空间直角坐标系
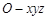，其中Ox//BC，Oy//AB，E为VC的中点.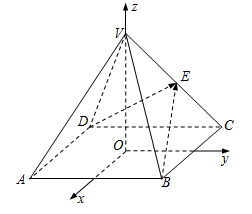
（1）用a和h表示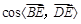
；
（2）当
是二面角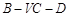
的平面角时，求cos
选修4—5：不等式选讲
设函数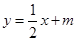
．
（1）当
时，求函数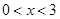
的定义域；
（2）若函数
的定义域为R，试求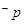
的取值范围．
选修4—4：坐标系与参数方程
在平面直角坐标系xOy中，以O为极点，Ox为极轴建立极坐标系，且两种坐标系长度单位一致. 已知直线l的极坐标方程为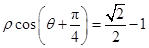
，圆C在直角坐标系中的参数方程为
（
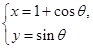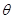为参数），求直线l与圆C的公共点的个数.