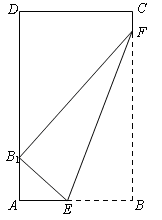
(本小题满分14分)矩形纸片ABCD的边AB=6,AD=10,点E、F分别在边AB和BC上(不含端点). 现将纸片的右下角沿EF翻折,使得顶点B翻折后的新位置B1恰好落在边AD上. 设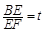 ,EF=l,l关于t的函数为
,EF=l,l关于t的函数为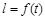 .
. 
试求:(1)函数f(t)的定义域;
(2)函数f(t)的最小值.
已知向量 =(
=(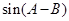 ,
, ),
), =(1,
=(1, ),且
),且

 =
=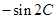 ,其中
,其中 、
、 、
、 分别为
分别为 的三边
的三边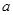 、
、 、
、 所对的角.
所对的角.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若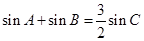 ,且
,且 ,求边
,求边 的长.
的长.
已知 ,函数
,函数
(1)求曲线 在点
在点 处的切线方程; (2)当
处的切线方程; (2)当 时,求
时,求 的最大值.
的最大值.
知椭圆 的左右焦点为F1,F2,离心率为
的左右焦点为F1,F2,离心率为 ,以线段F1 F2为直径的圆的面积为
,以线段F1 F2为直径的圆的面积为 , (1)求椭圆的方程;(2) 设直线l过椭圆的右焦点F2(l不垂直坐标轴),且与椭圆交于A、B两点,线段AB的垂直平分线交x轴于点M(m,0),试求m的取值范围.
, (1)求椭圆的方程;(2) 设直线l过椭圆的右焦点F2(l不垂直坐标轴),且与椭圆交于A、B两点,线段AB的垂直平分线交x轴于点M(m,0),试求m的取值范围.
已知 ,点
,点 在曲线
在曲线 上
上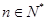 ,
, (Ⅰ)(Ⅰ)求数列
(Ⅰ)(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 的前n项和为
的前n项和为 ,若对于任意的
,若对于任意的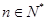 ,使得
,使得 恒成立,求最小正整数t的值.
恒成立,求最小正整数t的值.
如图,在四棱锥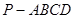 中,底面
中,底面 是矩形,
是矩形,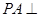 底面
底面 ,
, 是
是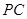 的中点,已知
的中点,已知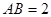 ,
, ,
,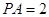 ,
,
求:(Ⅰ)三角形 的面积;(II)三棱锥
的面积;(II)三棱锥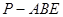 的体积
的体积