已知△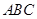 中,角
中,角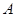 、
、 、
、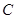 成等差数列,且
成等差数列,且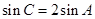 .
.
(1)求角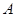 、
、 、
、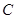 ;
;
(2)设数列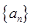 满足
满足 ,前
,前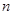 项为和
项为和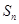 ,若
,若 ,求
,求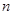 的值.
的值.
已知函数 .(1)求函数
.(1)求函数 的单调区间;
的单调区间;
(2)设函数 .若至少存在一个
.若至少存在一个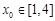 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知椭圆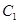 的中心在坐标原点,两个焦点分别为
的中心在坐标原点,两个焦点分别为 ,
,
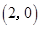 ,点
,点 在椭圆
在椭圆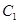 上,过点
上,过点 的直线
的直线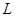 与抛物线
与抛物线 交于
交于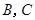 两点,抛物线
两点,抛物线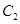 在点
在点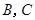 处的切线分别为
处的切线分别为 ,且
,且 与
与 交于点
交于点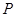 .
.
(1) 求椭圆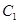 的方程;
的方程;
(2) 是否存在满足 的点
的点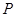 ? 若存在,指出这样的点
? 若存在,指出这样的点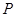 有几个(不必求出点
有几个(不必求出点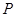 的坐标); 若不存在,说明理由.
的坐标); 若不存在,说明理由.
如图,正三棱柱 中,侧面
中,侧面 是边长为2的正方形,
是边长为2的正方形, 是
是 的中点,
的中点,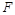 在棱
在棱 上.
上.
(1)当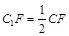 时,求三棱锥
时,求三棱锥 的体积.
的体积.
(2)当点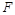 使得
使得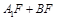 最小时,判断直线
最小时,判断直线 与
与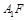 是否垂直,并证明结论.
是否垂直,并证明结论.
已知集合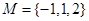 ,
, ,
, .从集合
.从集合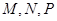 中各取一个元素分别记为
中各取一个元素分别记为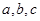 ,设方程
,设方程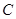 为
为 .
.
(1)求方程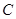 表示焦点在
表示焦点在 轴上的双曲线的概率.
轴上的双曲线的概率.
(2)求方程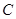 不表示椭圆也不表示双曲线的概率.
不表示椭圆也不表示双曲线的概率.