如图所示，坐标平面的第Ⅳ象限内存在大小为E、方向坚直向上的匀强电场，第I象限内存在磁感应强度大小为B、方向垂直纸面向里的匀强磁场。足够长的挡板MN垂直y轴放置且距原点O的距离为d。一质量为m(不计重力)、带电量为-q的粒子若自距原点O为L的A点以大小为
，方向沿x轴正方向的速度进入磁场，则粒子恰好到达O点而不进入电场。现该粒子仍从A点进入磁场，但初速度大小为
，为使粒子进入电场后能垂直打在挡板上，求粒子在A点进入磁场时： (1)其速度方向与y轴正方向之间的夹角。(2)粒子到达挡板上时的速度大小。
如图，直角坐标系
中，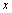
＜O的区域存在沿+
轴方向的匀强电场，场强大小为
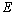，在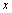＞0的区域存在一垂直纸面的矩形有界匀强磁场，其左边界和下边界分别与
、
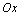轴重合，磁感应强度大小为
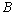(图中未画出)，现有一质量为
、电荷量为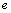
的电子从第二象限的某点P以一定初速度
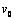(未知)沿+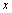轴方向开始运动，以
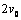的速度经过坐标为(O，L)的Q点，再经过磁场偏转恰好从坐标原点O沿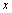轴的负方向返回电场，求：
(1)P点的坐标以及初速度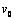为多少?
(2)矩形磁场区域的最小面积。
如图所示，在相互垂直的水平匀强电场和水平匀强磁场中，有一竖直固定绝缘杆
，小球P套在杆上，已知P的质量为
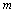，电荷量为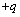
，P与杆间的动摩擦因数为
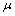，电场强度为
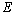，磁感应强度为
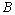，小球由静止起开始下滑，设电场、磁场区域足够大，杆足够长，求：
(1)当下滑加速度为最大加速度一半时球的速度；
(2)当下滑速度为最大下滑速度一半时球的加速度。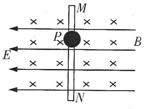
如图(甲)所示，一对平行放置的金属板M、N的中心各有一小孔P、Q，PQ连线垂直金属板；N板右侧的圆A内分布有方向垂直于纸面的匀强磁场，磁感应强度大小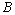为
，圆半径为
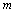，且圆心O在PQ的延长线上，现使置于P处的粒于源连续不断地沿PQ方向放出质量为
、电量为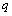
的带负电粒子(带电粒子的重力和初速度忽略不计，粒子间的相互作用力忽略不计)，从某一时刻开始，在板N、M间加上如图(乙)所示的交变电压，周期为T，电压大小为
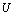，如果只有在每个周期的0～
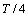时间内放出的带电粒子才能从小孔Q射出，求：
(1)平行金属板的板间距离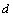
。
(2)带电粒子达到Q孔的速度范围．
(3)带电粒子通过该圆形磁场的最小偏转角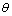
．
(甲)(乙)
如图所示，倾角θ=30º、宽度L=1m的足够长的“U”形平行光滑金属导轨固定在磁感应强度B =1T，范围足够大的匀强磁场中，磁场方向垂直于斜面向下。用平行于轨道的牵引力拉一根质量m =0.2㎏、电阻R =1Ω的垂直放在导轨上的金属棒a b，使之由静止开始沿轨道向上运动。牵引力做功的功率恒为6W，当金属棒移动2.8m时，获得稳定速度，在此过程中金属棒产生的热量为5.8J，不计导轨电阻及一切摩擦，取g=10m/s2。求：
（1）金属棒达到稳定时速度是多大？
（2）金属棒从静止达到稳定速度时所需的时间多长?
如图所示，把两根平行光滑金属导轨放在水平桌面上，桌子高0.8 m，导轨间距0.2 m，在导轨水平部分有磁感应强度为0.1 T，方向竖直向下的匀强磁场，弧形金属导轨的一端接有电阻R="1" Ω，质量m="0.2" kg的金属杆ab由静止开始距桌面h="0.2" m高处开始下滑，最后落到距桌子水平距离s="0.4" m处，金属杆及导轨电阻不计，试求：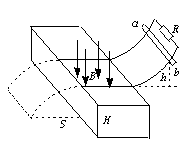
（1）金属杆进入导轨水平部分瞬间产生的感应电流的大小和方向.
(2)金属杆滑出导轨瞬间感应电动势的大小.
(3)整个过程中电阻R放出的热量.