如图所示，一位质量
参加“挑战极限”的业余选手，要越过一宽度为
的水沟，跃上高为
的平台．采用的方法是：人手握一根长
的轻质弹性杆一端，从
点由静止开始匀加速助跑，至
点时，杆另一端抵在O点的阻挡物上，接着杆发生形变、同时脚蹬地，人被弹起，到达最高点时杆处于竖直状态，人的重心在杆的顶端，此刻人放开杆水平飞出，最终趴落到平台上，运动过程中空气阻力可忽略不计．
（1）设人到达点时速度
，人匀加速运动的加速度
，求助跑距离SAB；
（2）人要到达平台，在最高点飞出时刻速度
至少多大？(取g=10m／s2)
（3）设人跑动过程中重心离地高度
，在(1)、(2)问的条件下，在B点蹬地弹起瞬间，人至少再做多少功？
如图所示，一个边长为L的正方形金属框，质量为m，电阻为R ．用细线把它悬挂于一个有界的磁场边缘。金属框的上半部处于磁场内，下半部处于磁场外。磁场随时间均匀变化满足B=kt规律。已知细线所能承受的最大拉力T=2mg．求从t=0时起，经多长时间细线会被拉断。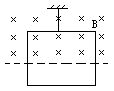
图为一个实验装置的俯视图，水平放置的两条光滑平行金属导轨相距为d。处在竖直的匀强磁场中，磁感强度为B，导轨左侧连有阻值为R的电阻，导轨上放有质量为m，阻值为r的导体MN，MN在水平恒力F作用下沿导轨向右运动。导轨电阻不计。求：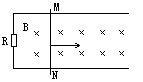
(1)导体MN可以达到的最大速度值。
(2)导体MN速度为量大速度的1/3时的加速度值。
(3)导体MN达到最大速度即撤去F，求这以后电阻R释放的焦耳热。
如图所示，U形金属框架MNQP放置在水平桌面上，MN与PQ的间距为0.3m，一根质量为57.6g的金属杆AC放置在框架上，且AQ=CN=0.6m，杆与框架的最大静摩擦力为0.288N，它与框架围成的回路总电阻为0.3Ω，有一与导轨平面垂直、磁感强度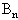
=3.25T的匀强磁场穿过导轨平面，若此磁场以0.4T/s的变化率均匀变化，经过多少时间才能使AC运动?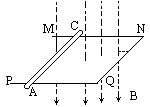
如图：倾斜水平轨道都为光滑轨道，水平轨道处在竖直向下的匀强磁场中，金属杆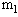
进入水平轨道瞬间速度为
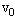，此时金属杆
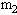处在静止状态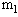，=3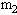水平轨道为无限长，两杆不能相碰，则两杆在轨道上运动的最终速度分别为多少?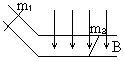
两根长为L的金属棒MN、PQ平行地放在水平导轨上．导轨电阻为零．MN和PQ的总电阻为R．匀强磁场B的方向如图所示．用力拉动MN，已知它在导轨上的速度达到v时，PQ(质量为m)才能够在导轨上匀速移动，求PQ与导轨间的动摩擦因数?