表演“顶杆”杂技时,一个人站在地上(称为“底人”)户上扛一长L=6m,质量m1=15kg的竹竿,一质量m2=45kg的演员(可当质点处理)在竿顶从静止开始先匀加速再匀减速下滑,下滑时加速度大小相等,下滑的总时间为t=3s,演员恰从杆顶滑至杆底部。求:
(1)演员下滑过程中的最大速度?
(2)演员在减速下滑过程中竹竿对“底”人的压力?
如图所示,质量M = 0.1kg的有孔小球穿在固定的足够长的斜杆上,斜杆与水平方向的夹角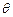 = 37°球与杆间的动摩擦因数
= 37°球与杆间的动摩擦因数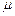 = 0.5。小球受到竖直向上的恒定拉力F = 1.2N后,由静止开始沿杆斜向上做匀加速直线运动。求(sin37°= 0.6,cos37° = 0.8,重力加速度g取10/s2):
= 0.5。小球受到竖直向上的恒定拉力F = 1.2N后,由静止开始沿杆斜向上做匀加速直线运动。求(sin37°= 0.6,cos37° = 0.8,重力加速度g取10/s2):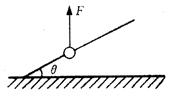
(1)斜杆对小球的滑坳摩擦力的大小;
(2)小球的加速度;
(3)最初2s内小球的位移。
一新车型赛车沿倾角为θ=370的专用长斜坡测试道进行测试,该车总质量为m=1t,由静止开始沿长斜坡向上运动,传感设备记录其运动的速度-时间图象(v-t图象)如图.该车运动中受到的摩擦阻力(含空气阻力)恒定,且摩擦阻力跟对路面压力的比值为μ=0.25.0~5s的v-t图线为直线,5s末起达到该车发动机的额定牵引功率并保持该功率行驶,在5s~20s之间,v-t图线先是一段曲线,后为直线.取g=10m/s2,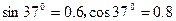 .求:
.求: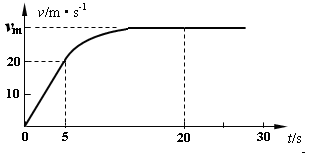
(1)该车发动机牵引力的额定功率;
(2)车的最大速度vm;
(3)该车出发后前20s的位移.
如图所示,两个几何形状完全相同的平行板电容器PQ和MN,水平置于水平方向的匀强磁场中(磁场区域足够大),两电容器极板左端和右端分别在同一竖直线上。已知P、Q之间和M、N之间的距离都是d,板间电压都是U,极极长度均为l。今有一电子从极板边缘的O点以速度v0沿沿P、Q两板间的中心线进入电容器,并做匀速直线运动穿过电容器,此后经过磁场偏转又沿水平方向进入到电容器M、N板间,在电容器M、N中也沿水平方向做匀速直线运动,穿过M、N板间的电场后,再经过磁场偏转又通过O点沿水平方向进入电容器P、Q极板间,循环往复。已知电子质量为m,电荷为e。
(1)试分析极板P、Q、M、N各带什么电荷?
(2)Q板和M板间的距离x满足什么条件时,能够达到题述过程的要求?
(3)电子从O点出发至第一次返回到O点经过了多长时间?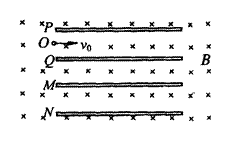
两根足够长的平行金属导轨,固定在同一水平面上,磁感应强度为B的匀强磁场与导轨所在平面垂直,方向竖直向下,导轨的电阻忽略不计,导轨间的距离为L,两根质量均为m的平行金属杆甲、乙可在导轨上无摩擦地滑动,滑动过程中与导轨保持垂直,每根金属杆接入回路的电阻都为R,在开始时刻,两杆都处于静止状态。现有一与导轨平行,大小为F的恒力作用于金属杆甲上,使金属杆在导轨上滑动。
(1)若某时刻甲的速度为v1,乙的速度为v2,求此时乙的加速度大小a乙;
(2)求由两金属杆与两金属导轨构成的回路中的最大感应电动势E。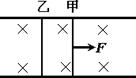

(1)通过电阻R的电流Ⅰ
(2)电阻R消耗的电功率P.