养路处建造圆锥形无底仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12 m,高4 m,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4 m(高不变);二是高度增加4 m (底面直径不变).
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积;
(3)哪个方案更经济些？
(1)解不等式
；
(2)如果关于
的不等式
的解集不是空集，求实数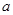
的取值范围.
已知复数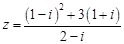
，若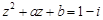
，
(1)求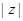
； (2)求实数
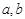的值.
已知关于x的不等式|x－3|+|x－4|< 3a2－7a+4．
（1）当a=2时，解上述不等式；
（2）如果关于x的不等式| x－3|+|x－4|< 23a2－7a+4的解集为空集，求实数a的取值范围．
已知⊙O1和⊙O2的极坐标方程分别是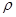
=2cos
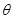和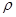="2a" sin
是非零常数）．
（1）将两圆的极坐标方程化为直角坐标方程；
（2）若两圆的圆心距为
，求a的值．
如图，AB、CD是⊙O的两条平行切线，B、D为切点，AC为⊙O的切线，切点为E．过A作AF⊥CD，F为垂足．
（1）求证：四边形ABDF是矩形；
（2）若AB=4，CD=9，求⊙O的半径．