(1)解不等式 ;
;
(2)如果关于 的不等式
的不等式 的解集不是空集,求实数
的解集不是空集,求实数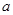 的取值范围.
的取值范围.
设数列 是各项均为正数的等比数列,其前
是各项均为正数的等比数列,其前 项和为
项和为 ,若
,若 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)对于正整数 (
( ),求证:“
),求证:“ 且
且 ”是“
”是“ 这三项经适当排序后能构成等差数列”成立的充要条件;
这三项经适当排序后能构成等差数列”成立的充要条件;
(3)设数列 满足:对任意的正整数
满足:对任意的正整数 ,都有
,都有
 ,且集合
,且集合 中有且仅有3个元素,试求
中有且仅有3个元素,试求 的取值范围.
的取值范围.
某地拟模仿图甲建造一座大型体育馆,其设计方案侧面的外轮廓线如图乙所示:曲线 是以点
是以点 为圆心的圆的一部分,其中
为圆心的圆的一部分,其中 (
( ,单位:米);曲线
,单位:米);曲线 是抛物线
是抛物线 的一部分;
的一部分; ,且
,且 恰好等于圆
恰好等于圆 的半径. 假定拟建体育馆的高
的半径. 假定拟建体育馆的高 米.
米.
(1)若要求 米,
米,
 米,求
米,求 与
与 的值;
的值;
(2)若要求体育馆侧面的最大宽度 不超过
不超过 米,求
米,求 的取值范围;
的取值范围;
(3)若 ,求
,求 的最大值.
的最大值.
(参考公式:若 ,则
,则 )
)
在平面直角坐标系 中,椭圆
中,椭圆 的右准线方程为
的右准线方程为 ,右顶点为
,右顶点为 ,
,
上顶点为 ,右焦点为
,右焦点为 ,斜率为
,斜率为 的直线
的直线 经过点
经过点 ,且点
,且点 到直线
到直线 的距离为
的距离为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)将直线 绕点
绕点 旋转,它与椭圆
旋转,它与椭圆 相交于另一点
相交于另一点 ,当
,当 三点共线时,试确定直线
三点共线时,试确定直线 的斜率.
的斜率.
如图,在正方体 中,
中, 分别为
分别为 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 .
.
在平面直角坐标系 中,设锐角
中,设锐角 的始边与
的始边与 轴的非负半轴重合,终边与单位圆交于点
轴的非负半轴重合,终边与单位圆交于点 ,将射线
,将射线 绕坐标原点
绕坐标原点 按逆时针方向旋转
按逆时针方向旋转 后与单位圆交于点
后与单位圆交于点 . 记
. 记 .
.
(1)求函数 的值域;
的值域;
(2)设 的角
的角 所对的边分别为
所对的边分别为 ,若
,若 ,且
,且 ,
, ,求
,求 .
.