设数列 是各项均为正数的等比数列,其前
是各项均为正数的等比数列,其前 项和为
项和为 ,若
,若 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)对于正整数 (
( ),求证:“
),求证:“ 且
且 ”是“
”是“ 这三项经适当排序后能构成等差数列”成立的充要条件;
这三项经适当排序后能构成等差数列”成立的充要条件;
(3)设数列 满足:对任意的正整数
满足:对任意的正整数 ,都有
,都有
 ,且集合
,且集合 中有且仅有3个元素,试求
中有且仅有3个元素,试求 的取值范围.
的取值范围.
(本小题满分13分) 我们知道:人们对声音有不同的感觉,这与它的强度有关系,声音的强度用
我们知道:人们对声音有不同的感觉,这与它的强度有关系,声音的强度用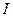 (单位:
(单位: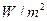 )表示,但在实际测量时,常用声音的强度水平
)表示,但在实际测量时,常用声音的强度水平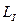 (单位:分贝)表示,它们满足公式:(
(单位:分贝)表示,它们满足公式:( ,其中
,其中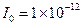 (
(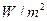 )),
)),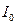 是人们能听到的最小强度,是听觉的开始.请回答以下问题:
是人们能听到的最小强度,是听觉的开始.请回答以下问题:
(Ⅰ)树叶沙沙声的强度为 (
(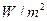 ),耳语的强度为
),耳语的强度为 (
(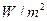 ),无线电广播的强度为
),无线电广播的强度为 (
(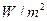 ),试分别求出它们的强度水平;
),试分别求出它们的强度水平;
(Ⅱ)某小区规定:小区内公共场所 的声音的强度水平必须保持在
的声音的强度水平必须保持在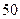 分贝以下(不含
分贝以下(不含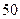 分贝),试求声音强度
分贝),试求声音强度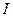 的取值范围.
的取值范围.
. (本小题满分13分)
(本小题满分13分)
在等比数列 中,
中, 已知
已知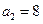 ,
, .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若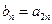 ,求数列
,求数列 的前
的前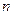
 项和
项和 .
.
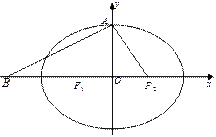
设椭圆 的左、右焦点分别为
的左、右焦点分别为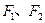 ,上顶点为
,上顶点为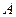 ,在
,在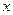 轴负半轴上有一点
轴负半轴上有一点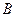 ,满足
,满足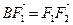 ,且
,且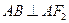 .
.
( 1)求椭圆
1)求椭圆 的离心率;
的离心率;
(2)若过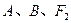 三点的圆恰好与
三点的圆恰好与 直线
直线 相切,求椭圆
相切,求椭圆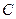 的方程;
的方程;
(3)在(2)的条件下,过右焦点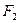 作斜率为
作斜率为
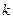 的直线
的直线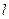 与椭圆
与椭圆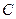 交于
交于 两点,在
两点,在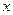 轴上是否存在点
轴上是否存在点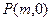 使得以
使得以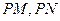 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出 的取值范围,如果不存在,说明理由。
的取值范围,如果不存在,说明理由。
设函数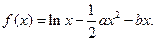
(1)当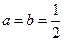 时,求
时,求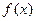 的最大值;
的最大值;
(2)令 ,(
,(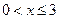 ),其图象上任意一点
),其图象上任意一点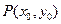 处切线的斜率
处切线的斜率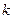 ≤
≤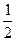 恒成立,求实数
恒成立,求实数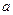 的取值范围;
的取值范围;
某射手每次射击击中目标的概率是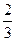 ,且各次射击的结果互不影响。
,且各次射击的结果互不影响。
(Ⅰ)假设这名射手射击5次,求恰有2次击中目标的概率
(Ⅱ)假设这名射手射击5次,求有3次连续击中目标。另外2次未击中目标的概率;
(Ⅲ)假设这名射手射击3次,每次射击, 击中目标得1分,未击中目标得0分,在3次射击中,若有2次连续击中,而
击中目标得1分,未击中目标得0分,在3次射击中,若有2次连续击中,而 另外1次未击中,则额外加1分;若3次全击中,则额外加3分,记
另外1次未击中,则额外加1分;若3次全击中,则额外加3分,记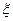 为射手射击3次后的总的分数,求
为射手射击3次后的总的分数,求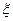 的分布列。
的分布列。