已知函数
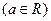，函数
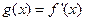
（1）判断方程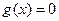
的零点个数；
（2）解关于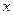
的不等式
，并用程序框图表示你的求解过程．
先阅读下列不等式的证法，再解决后面的问题：已知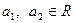
，
，求证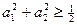
．
证明：构造函数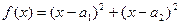
，
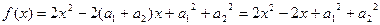
因为对一切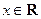
，恒有
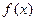≥0，所以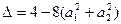
≤0，从而得，
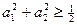（1）若
，
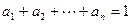，请写出上述结论的推广式；
（2）参考上述解法，对你推广的结论加以证明．
蜜蜂被认为是自然界中最杰出的建筑师，单个蜂巢可以近似地看作是一个正六边形，如图为一组蜂巢的截面图．其中第一个图有1个蜂巢，第二个图有7个蜂巢，第三个图有19个蜂巢，按此规律，以
表示第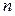
幅图的蜂巢总
数．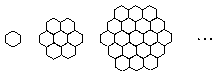
（1）试给出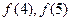
的值，并求的表达式（不要求证明）；
（2）证明：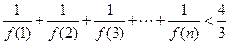
．
P为椭圆
＝1(a＞b＞0)上一点，F1为它的一个焦点，求证：以PF1为直径的圆与以长轴为直径的圆相切．
已知双曲线的一个焦点为(－1，－1)，相应准线是x＋y－1＝0，且双曲线过点(－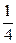
，0)．求双曲线的方程．
，
，求
的值．