在直角坐标系 中,圆
中,圆 的参数方程为
的参数方程为 (
(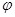 为参数),以
为参数),以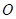 为极点,
为极点,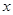 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求曲线 的极坐标方程;
的极坐标方程;
(2)设直线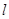 的极坐标方程是
的极坐标方程是 ,射线
,射线 与圆
与圆 的交点为
的交点为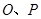 ,与直线
,与直线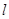 的交点为
的交点为 ,求线段
,求线段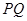 的长.
的长.
将双曲线C:x2-y2=1上点绕原点逆时针旋转45°,得到新图形C′,试求C′的方程.
已知二阶矩阵M有特征值 =8及对应的一个特征向量e1=
=8及对应的一个特征向量e1= ,并且矩阵M对应的变换将点(-1,2)变换成(-2,4).
,并且矩阵M对应的变换将点(-1,2)变换成(-2,4).
(1)求矩阵M;
(2)求矩阵M的另一个特征值及对应的一个特征向量e2的坐标之间的关系.
试从几何变换的角度求AB的逆矩阵.
(1)A= ,B=
,B= ;
;
(2)A= ,B=
,B= .
.
已知O(0,0),A(2,1),O,A,B,C依逆时针方向构成正方形的四个顶点.
(1)求B,C两点的坐标;
(2)把正方形OABC绕点A按顺时针方向旋转45°得到正方形AB′C′O′,求B′,C′,O′三点的坐标.
已知变换T把平面上的点A(2,0),B(3,1)分别变换成点A′(2,1),B′(3,2),试求变换T对应的矩阵M.