试从几何变换的角度求AB的逆矩阵.
(1)A= ,B=
,B= ;
;
(2)A= ,B=
,B= .
.
已知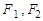 为双曲线
为双曲线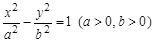 的左、右焦点.
的左、右焦点.
(Ⅰ)若点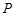 为双曲线与圆
为双曲线与圆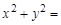
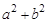 的一个交点,且满足
的一个交点,且满足 ,求此双曲线的离心率;
,求此双曲线的离心率;
(Ⅱ)设双曲线的渐近线方程为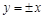 ,
,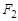 到渐近线的距离是
到渐近线的距离是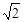 ,过
,过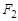 的直线交双曲线于A,B两点,且以AB为直径的圆与
的直线交双曲线于A,B两点,且以AB为直径的圆与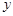 轴相切,求线段AB的长.
轴相切,求线段AB的长.
已知函数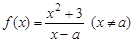 ,其中
,其中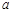 为非零常数.
为非零常数.
(Ⅰ)解关于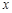 的不等式
的不等式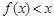 ;
; (Ⅱ)若当
(Ⅱ)若当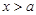 时,函数
时,函数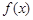 的最小值为3,求实数
的最小值为3,求实数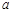 的值.
的值.
已知抛物线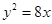 的准线与x轴交于点Q.
的准线与x轴交于点Q.
(Ⅰ)若过点Q的直线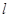 与抛物线有公共点,求直线
与抛物线有公共点,求直线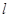 的斜率的取值范围;
的斜率的取值范围;
(Ⅱ)若过点Q的直线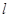 与抛物线交于不同的两点A、B,求AB中点P的轨迹方程.
与抛物线交于不同的两点A、B,求AB中点P的轨迹方程.
(Ⅰ)已知双曲线C与双曲线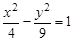 有相同的渐近线,且一条准线为
有相同的渐近线,且一条准线为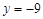 ,求双曲线C的方程;
,求双曲线C的方程; (Ⅱ)已知圆截
(Ⅱ)已知圆截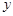 轴所得弦长为6,圆心在直线
轴所得弦长为6,圆心在直线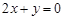 上,并与
上,并与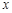 轴相切,求该圆的方程.
轴相切,求该圆的方程.
已知直线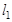 :
: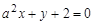 ,直线
,直线 :
: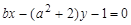 .若
.若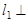
 ,求
,求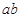 的取值范围.
的取值范围.