求两条平行线l1:6x+8y=20和l2:3x+4y-15=0的距离.
(本小题满分12分)
已知函数
(1)求 的最小正周期
的最小正周期
(2)求 的的最大值和最小值;
的的最大值和最小值;
(3) 求 的的单调增区间
的的单调增区间
已知过点 的动直线
的动直线 与圆
与圆 :
: 相交于
相交于 、
、 两点,
两点, 是
是 中点,
中点, 与直线
与直线 :
: 相交于
相交于 .
.
(1)求证:当 与
与 垂直时,
垂直时, 必过圆心
必过圆心 ;
;
(2)当 时,求直线
时,求直线 的方程;
的方程;
(3)探索 是否与直线
是否与直线 的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
设 为奇函数,
为奇函数, 为常数。
为常数。
(1)求 的值;
的值;
(2)证明: 在(1,+∞)内单调递增;
在(1,+∞)内单调递增;
(3)若对于[3,4]上的每一个 的值,不等式
的值,不等式 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
如图,在直三棱柱 中,
中, ,
,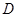 为
为 中点.
中点.
(1)求证: ;
;
(2)求证:  ∥平面
∥平面 ;
;
(3)求二面角 的余弦值.
的余弦值.
(12分)某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响. 已知学生小张只选甲的概率为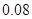 ,只选修甲和乙的概率是
,只选修甲和乙的概率是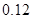 ,至少选修一门的概率是
,至少选修一门的概率是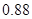 ,用
,用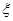 表示小张选修的课程门数和没有选修的课程门数的乘积.
表示小张选修的课程门数和没有选修的课程门数的乘积.
(Ⅰ)求学生小张选修甲的概率;
(Ⅱ)记“函数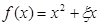 为
为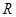 上的偶函数”为事件
上的偶函数”为事件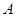 ,求事件
,求事件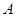 的概率;
的概率;
(Ⅲ)求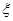 的分布列和数学期望;
的分布列和数学期望;