如图所示,在四棱锥P—ABCD中,底面是边长为2的菱形,∠DAB=60°,
对角线AC与BD交于点O,PO⊥平面ABCD,PB与平面ABCD所成角为60°.
(1)求四棱锥的体积;
(2)若E是PB的中点,求异面直线DE与PA所成角的余弦值.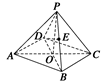
(本小题8分)在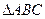 中,试证明等式:
中,试证明等式: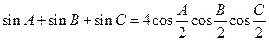 .
.
(本小题8分)规定记号“※”表示一种运算,即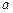 ※
※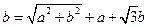 ,
,
记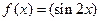 ※
※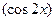 .
.
(1)求函数 的表达式和它的最小正周期;
的表达式和它的最小正周期;
(2)若函数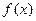 在
在 处取到最大值,求
处取到最大值,求 的值
的值
椭圆的中心在原点,焦点F在 轴上,离心率为
轴上,离心率为 ,点
,点 到F点的距离为
到F点的距离为 ,(1)求椭圆的方程;
,(1)求椭圆的方程;
(2)直线 与椭圆交于不同的两点M、N两点,若
与椭圆交于不同的两点M、N两点,若 ,求实数
,求实数 的取值范围。
的取值范围。
双曲线的中心在原点,焦点在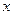 轴上,实轴长为4,它的两条渐近线与以
轴上,实轴长为4,它的两条渐近线与以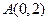 为圆心,1为半径的圆相切,直线
为圆心,1为半径的圆相切,直线 过点A与双曲线的右支交于B、C两点,
过点A与双曲线的右支交于B、C两点,
(1)求双曲线的方程;(2)若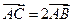 ,求直线
,求直线 的方程
的方程
如图:在四棱锥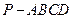 中,底面为菱形,
中,底面为菱形,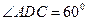 ,
,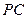 与底面
与底面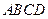 垂直,
垂直,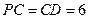 ,
,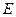 为棱
为棱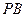 的中点,
的中点,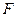 为
为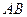 的中点,
的中点,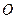 为
为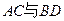 的交点,
的交点,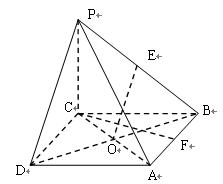
(1)求证: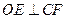 ;
;
(2)求锐二面角 的余弦值.
的余弦值.