(本小题8分)规定记号“※”表示一种运算,即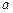 ※
※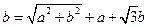 ,
,
记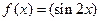 ※
※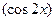 .
.
(1)求函数 的表达式和它的最小正周期;
的表达式和它的最小正周期;
(2)若函数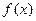 在
在 处取到最大值,求
处取到最大值,求 的值
的值
甲、乙、丙三人进行某项比赛,每局有两人参加,没有平局,在一局比赛中,甲胜乙的概率为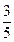 ,甲胜丙的概率为
,甲胜丙的概率为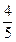 ,乙胜丙的概率为
,乙胜丙的概率为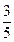 ,比赛的规则是先由甲和乙进行第一局的比赛,然后每局的获胜者与未参加此局比赛的人进行下一局的比赛,在比赛中,有人获胜两局就算取得比赛的胜利,比赛结束.
,比赛的规则是先由甲和乙进行第一局的比赛,然后每局的获胜者与未参加此局比赛的人进行下一局的比赛,在比赛中,有人获胜两局就算取得比赛的胜利,比赛结束.
(I)求只进行两局比赛,甲就取得胜利的概率;
(II)求只进行两局比赛,比赛就结束的概率;
(III)求甲取得比赛胜利的概率.
某市举行的一次数学新课程骨干培训,共邀请15名使用不同版本教材的教师,数据如下表所示:
| 版本 |
人教A版 |
人教B版 |
||
| 性别 |
男教师 |
女教师 |
男教师 |
女教师 |
| 人数 |
6 |
3 |
4 |
2 |
(Ⅰ)从这15名教师中随机选出2名,则2人恰好是教不同版本的男教师的概率是多少?
(Ⅱ)培训活动随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为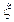 ,求随机变量
,求随机变量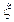 的分布列和数学期望
的分布列和数学期望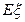 .
.
如图,在某城市中,M,N两地之间有整齐的方格形道路网,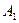 、
、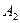 、
、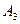 、
、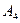 是道路网中位于一条对角线上的4个交汇处,今在道路网M、N处的甲、乙两人分别要到M,N处,他们分别随机地选择一条沿街的最短路径,同时以每10分钟一格的速度分别向N,M处行走,直到到达N,M为止。
是道路网中位于一条对角线上的4个交汇处,今在道路网M、N处的甲、乙两人分别要到M,N处,他们分别随机地选择一条沿街的最短路径,同时以每10分钟一格的速度分别向N,M处行走,直到到达N,M为止。
(1)求甲经过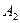 的概率;
的概率;
(2)求甲、乙两人相遇经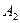 点的概率;
点的概率;
(3)求甲、乙两人相遇的概率;
旅游公司为3个旅游团提供4条旅游线路,每个旅游团任选其中一条.  (1)求3个旅游团选择3条不同的线路的概率
(1)求3个旅游团选择3条不同的线路的概率
(2)求恰有2条线路没有被选择的概率.
(3)求选择甲线路旅游团数的期望.
一纸箱中装有大小相等,但已编有不同号码的白色和黄色乒乓球,其中白色乒乓球有6个,黄色乒乓球有2个。
(Ⅰ)从中任取2个乒乓球,求恰好取得1个黄色乒乓球的概率;
(Ⅱ)每次不放回地抽取一个乒乓球,求第一次取得白色乒乓球时已取出的黄色乒乓球个数ξ的分布列及数学期望Eξ。