某市举行的一次数学新课程骨干培训,共邀请15名使用不同版本教材的教师,数据如下表所示:
| 版本 |
人教A版 |
人教B版 |
||
| 性别 |
男教师 |
女教师 |
男教师 |
女教师 |
| 人数 |
6 |
3 |
4 |
2 |
(Ⅰ)从这15名教师中随机选出2名,则2人恰好是教不同版本的男教师的概率是多少?
(Ⅱ)培训活动随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为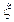 ,求随机变量
,求随机变量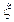 的分布列和数学期望
的分布列和数学期望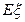 .
.
已知△ 的内角
的内角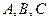 所对的边分别为
所对的边分别为 且
且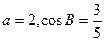 .
.
(1) 若 , 求
, 求 的值;
的值;
(2) 若△ 的面积
的面积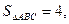 求
求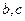 的值.
的值.
设条件p:2x2-3x+1≤0,条件q:x2-(2a+1)x+a(a+1)≤0,若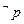 是
是 的必要不充分条件,求实数a的去值范围.
的必要不充分条件,求实数a的去值范围.
已知函数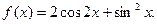
(1)求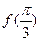 的值;
的值;
(2)求 的最大值和最小值。
的最大值和最小值。
(本题12分)
如图1所示,在平行六面体ABCD—A 1B1C1D1中,已知AB=5,AD=4,AA1=3
1B1C1D1中,已知AB=5,AD=4,AA1=3 ,AB⊥AD,∠A1AB=∠A1AD=
,AB⊥AD,∠A1AB=∠A1AD=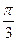 。(1)求证:顶点A1在底面ABCD上的射影O在∠BAD
。(1)求证:顶点A1在底面ABCD上的射影O在∠BAD 的平分线上;
的平分线上;
(2)求这个平行六面体的体积。
图1
(本题12分)
在单位正方体 中,M,N,
中,M,N, P分别是
P分别是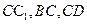 的中点,O为底面ABCD的中心.
的中点,O为底面ABCD的中心.
( 1)求证:OM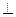 平面
平面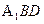 ;
;
(2)平面MNP 平面
平面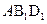 ;
;
(3)求B到平面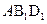 的距离
的距离