如图,在某城市中,M,N两地之间有整齐的方格形道路网,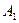 、
、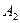 、
、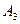 、
、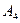 是道路网中位于一条对角线上的4个交汇处,今在道路网M、N处的甲、乙两人分别要到M,N处,他们分别随机地选择一条沿街的最短路径,同时以每10分钟一格的速度分别向N,M处行走,直到到达N,M为止。
是道路网中位于一条对角线上的4个交汇处,今在道路网M、N处的甲、乙两人分别要到M,N处,他们分别随机地选择一条沿街的最短路径,同时以每10分钟一格的速度分别向N,M处行走,直到到达N,M为止。
(1)求甲经过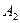 的概率;
的概率;
(2)求甲、乙两人相遇经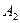 点的概率;
点的概率;
(3)求甲、乙两人相遇的概率;
(本小题满分14分)已知抛物线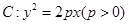 的焦点为
的焦点为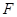 ,准线
,准线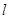 与
与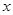 轴的交点为
轴的交点为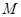 .点
.点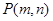 (
( )在抛物线
)在抛物线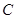 上,且
上,且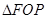 的外接圆圆心到准线
的外接圆圆心到准线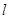 的距离为
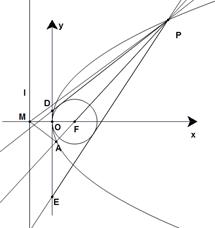
的距离为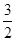 .
.
(Ⅰ)求抛物线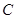 的方程;
的方程;
(Ⅱ)若直线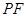 与抛物线
与抛物线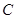 交于另一点
交于另一点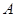 ,证明:
,证明: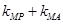 为定值;
为定值;
(Ⅲ)过点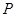 作圆
作圆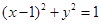 的两条切线,与
的两条切线,与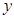 轴分别交于
轴分别交于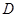 、
、 两点,求
两点,求 面积取得最小值时对应的
面积取得最小值时对应的 值.
值.
(本小题满分13分)已知函数 .
.
(Ⅰ)求函数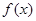 的单调区间;
的单调区间;
(Ⅱ)是否存在实数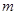 ,使得当
,使得当 时,对任意的
时,对任意的 ,恒有
,恒有 ?若存在,试求出实数
?若存在,试求出实数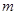 的取值范围,若不存在,试说明理由.
的取值范围,若不存在,试说明理由.
(本小题满分12分) 已知数列 的前
的前 项和为
项和为 ,数列
,数列 是公比为2的等比数列,且
是公比为2的等比数列,且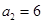 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若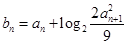 ,数列
,数列 的前
的前 项和为
项和为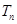 ,求使
,求使 成立的最小正整数
成立的最小正整数 .
.
(本小题满分12分)如图三棱锥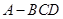 中,
中, ,
,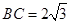 ,
,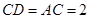 ,
,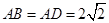 .
.
证明:(Ⅰ)面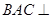 面
面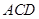 ;
;
(Ⅱ)求二面角 的余弦值..
的余弦值..
(本小题满分12分)党的十八大报告提出:要提高人民健康水平,改革和完善食品药品安全监管体制机制.为加大监督力度,某市工商部门对本市甲、乙两家小型食品加工厂进行了突击抽查,从两个厂家生产的产品中分别随机抽取各10件样品,测量该产品中某种微量元素的含量(单位:毫克),所得测量数据如图:
根据食品安全法规定:优等品中的此种微量元素含量不小于15毫克.
(Ⅰ)从甲食品加工厂抽出的上述10件样品中,随机抽取4件,求抽到的4件产品中优等品数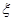 的分布列及其数学期望
的分布列及其数学期望 ;
;
(Ⅱ)若从甲、乙两个食品加工厂的10件样品中分别任意抽取3件,求甲、乙食品加工厂抽到的优等品数恰相同的概率.