如图所示，在四棱锥P—ABCD中，底面ABCD是∠DAB=60°且边长为a的菱形，侧面PAD为正三角形，其所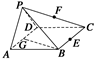 
在平面垂直于底面ABCD，若G为AD边的中点，
（1）求证：BG⊥平面PAD；
（2）求证：AD⊥PB；
（3）若E为BC边的中点，能否在棱PC上找到一点F，使平面DEF⊥平面ABCD，并证明你的结论.
（本小题满分12分）
已知正项等差数列
的前
项和为
，且满足
，
．
(Ⅰ)求数列的通项公式
；
（Ⅱ）若数列
满足
且
，求数列
的前项和
．
（本小题满分12分）
设
，函数
的定义域为
且
，
当
时有
（1）求
；
（2）求
的值；
（3）求函数
的单调区间．
（本小题满分12分）
已知向量
=（1,1），向量
与向量夹角为
，且
=－1.
（1）求向量
；
（2）若向量
与向量
=（1，0）的夹角为
，向量
=(cosA,2cos2
)，其中A、B、C为△ABC的内角，且B=60°，求|
|的取值范围；
（本小题满分12分）
现有四分之一圆形的纸板（如图），
，圆半径为
，要裁剪成四边形
，且满足
，
，
，记此四边形的面积为
，求的最大值．
（本小题满分12分）
已知平面上三个向量
，其中
，
（1）若
，且
∥
，求的坐标；
（2）若
，且
，求与
夹角的余弦值.