(本小题满分12分)
已知平面上三个向量 ,其中
,其中 ,
,
(1)若 ,且
,且 ∥
∥ ,求
,求 的坐标;
的坐标;
(2)若 ,且
,且 ,求
,求 与
与 夹角的余弦值.
夹角的余弦值.
已知双曲线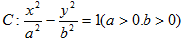 与椭圆
与椭圆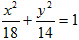 有共同的焦点,点
有共同的焦点,点 在双曲线
在双曲线 上.
上.
(1)求双曲线 的方程;
的方程;
(2)以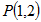 为中点作双曲线
为中点作双曲线 的一条弦
的一条弦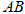 ,求弦
,求弦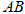 所在直线的方程.
所在直线的方程.
设命题p:(4x-3)2≤1;命题q:x2-(2a+1)x+a(a+1)≤0,若 p是
p是 q的必要不充分条件,求实数a的取值范围.
q的必要不充分条件,求实数a的取值范围.
已知函数 .
.
(1)解不等式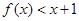 ;
;
(2)若对于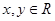 ,有
,有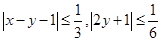 .求证:
.求证: .
.
在直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为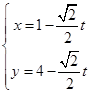 (t为参数),再以原点为极点,以x正半轴为极轴建立坐标系,并使得它与直角坐标系有相同的长度单位,在该极坐标系中圆C的方程为
(t为参数),再以原点为极点,以x正半轴为极轴建立坐标系,并使得它与直角坐标系有相同的长度单位,在该极坐标系中圆C的方程为 .
.
(1)求圆C的直角坐标方程;
(2)设圆C与直线 将于点
将于点 、
、 ,若点
,若点 的坐标为
的坐标为 ,求
,求 的值.
的值.
如图,圆 与圆
与圆 内切于点
内切于点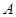 ,其半径分别为3与2,圆
,其半径分别为3与2,圆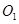 的弦
的弦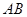 交圆
交圆 于点
于点 (
(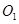 不在
不在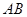 上),
上),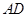 是圆
是圆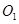 的一条直径.
的一条直径.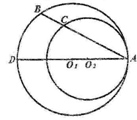
(1)求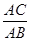 的值;
的值;
(2)若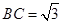 ,求
,求 到弦
到弦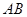 的距离.
的距离.