如图所示,四棱锥P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD= ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
(1)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(2)求证:无论点E在BC边的何处,都有PE⊥AF;
(3)当BE为何值时,PA与平面PDE所成角的大小为45°.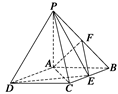
(本小题满分14分)
已知 是数列
是数列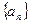 的前
的前 项和,且
项和,且 ,
, 时有
时有 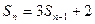 .
.
(1)求证 是等比数列;
是等比数列;
(2)求数列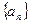 的通项公式.
的通项公式.
(本小题满分14分)已知向量 ,且与向量
,且与向量 的夹角为
的夹角为 ,其中
,其中 是
是 的内角.
的内角.
(1)求角 的大小;(2)求
的大小;(2)求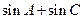 的取值范围.
的取值范围.
(本小题满分12分)
某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用 平均建筑费用
平均建筑费用 平均购地费用,平均购地费用
平均购地费用,平均购地费用 )
)
(本小题满分12分)
已知函数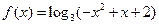 的定义域为集合
的定义域为集合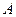 ,
,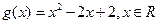 的值域为集合
的值域为集合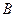 ,
,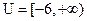 .(1)求
.(1)求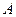 和
和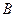 ; (2)求
; (2)求 、
、 .
.
(本小题满分14分)给定函数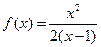
(1)试求函数 的单调减区间;
的单调减区间;
(2)已知各项均为负的数列 满足,
满足,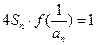 求证:
求证: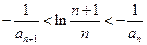 ;
;
(3)设 ,
,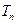 为数列
为数列 的前
的前 项和,求证:
项和,求证: 。
。