袋中有4个红球,3个黑球,从袋中随机地抽取4个球,设取到一个红球得2分,取到一个黑球得1分.
(1)求得分X的概率分布;
(2)求得分大于6的概率.
(本小题满分12分)某实验室一天的温度(单位:℃)随时间t(单位:h)的变化近似满足函数关系: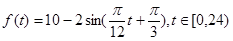 .
.
(1)求实验室这一天的最大温差;
(2)若要求实验室温度不高于11 ℃,则在哪段时间实验室需要降温?
【原创】(本小题满分12分)函数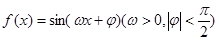 在同一个周期内,当
在同一个周期内,当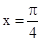 时,y取最大值1,当
时,y取最大值1,当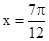 时,y取最小值-1.
时,y取最小值-1.
(1)求函数的解析式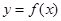 ;
;
(2)函数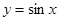 的图象经过怎样的变换可得到
的图象经过怎样的变换可得到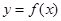 的图象?
的图象?
(3)若函数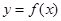 满足方程
满足方程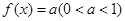 ,求在
,求在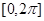 内的所有实数根之和.
内的所有实数根之和.
(本小题满分12分)设函数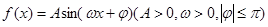 的图象的最高点D的坐标为(2,
的图象的最高点D的坐标为(2,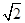 ),由最高点运动到相邻的最低点F时,曲线与x轴相交于点E(6,0).
),由最高点运动到相邻的最低点F时,曲线与x轴相交于点E(6,0).
(1)求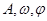 的值;
的值;
(2)求函数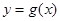 ,使其图象与
,使其图象与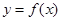 图象关于直线
图象关于直线 对称.
对称.
【原创】求证:
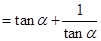 。
。
已知 是方程
是方程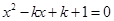 的两实根,求
的两实根,求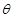 的值。
的值。