已知 是方程
是方程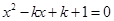 的两实根,求
的两实根,求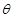 的值。
的值。
如图棱柱 的侧面
的侧面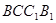 是菱形,
是菱形, ,D是
,D是 的中点,证明:
的中点,证明:
(Ⅰ)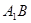 ∥面
∥面
(Ⅱ)平面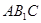
 平面
平面 .
.
已知函数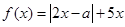 ,其中实数
,其中实数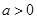 .
.
(1)当 时,求不等式
时,求不等式 的解集;
的解集;
(2)若不等式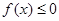 的解集为
的解集为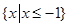 ,求
,求 的值.
的值.
在直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点 为极点,
为极点, 轴的正半轴为极轴的极坐标系下,曲线
轴的正半轴为极轴的极坐标系下,曲线 的方程为
的方程为 .
.
(1)求曲线 的普通方程和曲线
的普通方程和曲线 的直角坐标方程;
的直角坐标方程;
(2)设曲线 和曲线
和曲线 的交点
的交点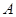 、
、 ,求
,求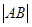 .
.
如图,点 是以线段
是以线段 为直径的圆
为直径的圆 上一点,
上一点,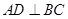 于点
于点 ,过点
,过点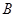 作圆
作圆 的切线,与
的切线,与 的延长线交于点
的延长线交于点 ,点
,点 是
是 的中点,连结
的中点,连结 并延长与
并延长与 相交于点
相交于点 ,延长
,延长 与
与 的延长线相交于点
的延长线相交于点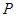 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求证: 是圆
是圆 的切线.
的切线.
已知圆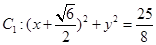 ,圆
,圆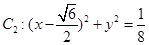 ,动圆
,动圆 与已知两圆都外切.
与已知两圆都外切.
(1)求动圆的圆心 的轨迹
的轨迹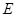 的方程(2)直线
的方程(2)直线 与点
与点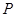 的轨迹
的轨迹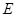 交于不同的两点
交于不同的两点 、
、 ,
,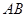 的中垂线与
的中垂线与 轴交于点
轴交于点 ,求点
,求点 的纵坐标的取值范围.
的纵坐标的取值范围.