1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球,现随机地从1号箱中取出一球放入2号箱,然后从2号箱随机取出一球,问
(1)从1号箱中取出的是红球的条件下,从2号箱取出红球的概率是多少?
(2)从2号箱取出红球的概率是多少?
(本小题共13分)
如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30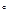 ,相距10海里C处的乙船.
,相距10海里C处的乙船.
(Ⅰ)求处于C处的乙船和遇险渔船间的距离;
(Ⅱ)设乙船沿直线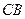 方向前往
方向前往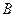 处救援,其方向与
处救援,其方向与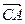 成
成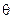 角,
角,
求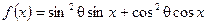 (x∈
(x∈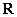 )的值域.
)的值域.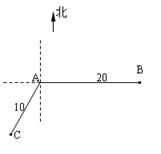
如图, 为双曲线 : 的右焦点。 为双曲线 右支上一点,且位于 轴上方, 为左准线上一点, 为坐标原点。已知四边形 为平行四边形, .
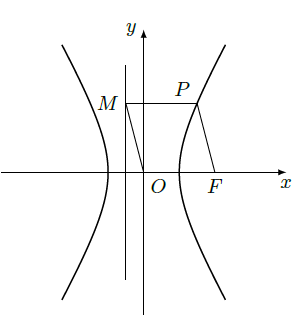
(Ⅰ)写出双曲线
的离心率
与
的关系式;
(Ⅱ)当
时,经过焦点
且品行于
的直线交双曲线于
、
点,若
,求此时的双曲线方程.
数列 的前 项和为 ,已知
(Ⅰ)写出 与 的递推关系式 ,并求 关于 的表达式;
(Ⅱ)设 ,求数列 的前 项和 .
已知函数 在 上有定义,对任何实数 和任何实数 ,都有
(Ⅰ)证明 ;
(Ⅱ)证明
,其中
和
均为常数;
(Ⅲ)当(Ⅱ)中的
时,设
,讨论
在
内的单调性并求极值.
如图, 是边长为1的正六边形 所在平面外一点, , 在平面 内的射影为 的中点 .

(Ⅰ)证明
;
(Ⅱ)求面
与面
所成二面角的大小.