)某篮球队与其他6支篮球队依次进行6场比赛,每场均决出胜负,设这支篮球队与其他篮球队比赛胜场的事件是独立的,并且胜场的概率是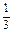 .
.
(1)求这支篮球队首次胜场前已经负了两场的概率;
(2)求这支篮球队在6场比赛中恰好胜了3场的概率;
(3)求这支篮球队在6场比赛中胜场数的期望和方差.
(本小题满分10分)
已知抛物线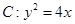 与直线
与直线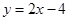 交于
交于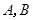 两点.
两点.
(Ⅰ)求弦 的长度;
的长度;
(Ⅱ)若点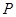 在抛物线
在抛物线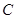 上,且
上,且 的面积为
的面积为 ,求点P的坐标.
,求点P的坐标.
(本小题满分12分)
在如图的多面体中,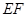 ⊥平面
⊥平面 ,
,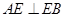 ,
,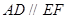 ,
,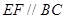 ,
,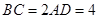 ,
,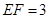 ,
,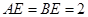 ,
, 是
是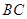 的中点.
的中点.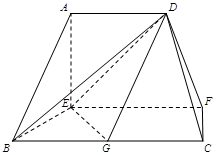
(Ⅰ) 求证: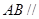 平面
平面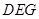 ;
;
(Ⅱ) 求二面角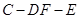 的余弦值.
的余弦值.
如图,设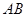 、
、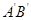 分别是圆
分别是圆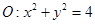 和椭圆
和椭圆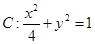 的弦,且弦的端点在
的弦,且弦的端点在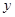 轴的异侧,端点
轴的异侧,端点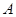 与
与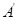 、
、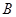 与
与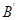 的横坐标分别相等,纵坐标分别同号.
的横坐标分别相等,纵坐标分别同号.
(Ⅰ)若弦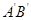 所在直线斜率为
所在直线斜率为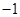 ,且弦
,且弦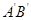 的中点的横坐标为
的中点的横坐标为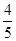 ,求直线
,求直线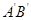 的方程;
的方程;
(Ⅱ)若弦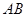 过定点
过定点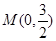 ,试探究弦
,试探究弦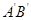 是否也必过某个定点. 若有,请证明;若没有,请说明理由.
是否也必过某个定点. 若有,请证明;若没有,请说明理由.
如图,有一边长为2米的正方形钢板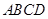 缺损一角(图中的阴影部分),边缘线
缺损一角(图中的阴影部分),边缘线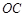 是以直线
是以直线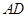 为对称轴,以线段
为对称轴,以线段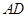 的中点
的中点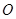 为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.
为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.
(Ⅰ)请建立适当的直角坐标系,求阴影部分的边缘线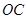 的方程;
的方程;
(Ⅱ)如何画出切割路径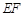 ,使得剩余部分即直角梯形
,使得剩余部分即直角梯形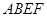 的面积最大?
的面积最大?
并求其最大值.
(本小题满分12分)
已知直线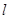 经过抛物线
经过抛物线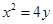 的焦点,且与抛物线交于
的焦点,且与抛物线交于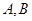 两点,点
两点,点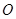 为坐标原点.
为坐标原点.
(Ⅰ)证明: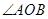 为钝角.
为钝角.
(Ⅱ)若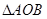 的面积为
的面积为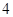 ,求直线
,求直线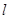 的方程;
的方程;