一个袋中装有若干个大小相同的黑球、白球和红球.已知从袋中任意摸出1个球,得到黑球的概率是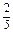 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是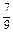 .若袋中共有10个球,
.若袋中共有10个球,
(1)求白球的个数;
(2)从袋中任意摸出3个球,记得到白球的个数为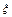 ,求随机变量
,求随机变量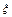 的数学期望E(
的数学期望E(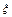 ).
).
(本小题满分14分)
已知数列 中,
中,
(1)求证:数列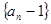 是等比数列;
是等比数列;
(2)设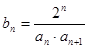 ,求证:数列
,求证:数列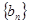 的前
的前 项和
项和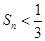 .
.
(3)比较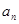 与
与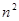 的大小(
的大小(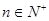 )。
)。
如图,在底面是正方形的四棱锥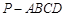 中,
中,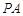
 面
面 ,
, 交
交 于点
于点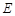 ,
, 是
是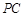 中点,
中点,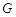 为
为 上一点.
上一点.
⑴求证: ;
;
⑵确定点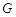 在线段
在线段 上的位置,使
上的位置,使 //平面
//平面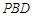 ,并说明理由.
,并说明理由.
⑶当二面角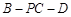 的大小为
的大小为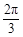 时,求
时,求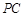 与底面
与底面 所成角的正切值.
所成角的正切值.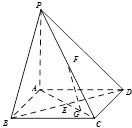
(本题满分12分)
2010年上海世博会上展馆 与展馆
与展馆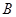 位于观光路的同侧,在观光路上相距
位于观光路的同侧,在观光路上相距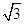 千米的
千米的 两点分别测得
两点分别测得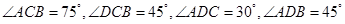 ,(
,(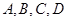 在同一平面内),求展馆
在同一平面内),求展馆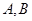 之间的距离.
之间的距离. 
(本小题满分12分)
已知函数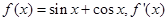 是
是 的导函数.
的导函数.
(1)若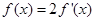 ,求
,求 的值.
的值.
(2)求函数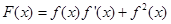 (
(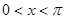 )的单调增区间。
)的单调增区间。
(本小题满分12分)已知函数 (
(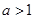 ).
).
(1)试讨论 在区间
在区间 上的单调性;
上的单调性;
(2)当 时,曲线
时,曲线 上总存在相异两点
上总存在相异两点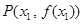 ,
, ,使得曲线
,使得曲线 在点
在点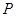 ,
, 处的切线互相平行,求证:
处的切线互相平行,求证: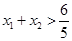 .
.