为了了解小学生的体能情况，抽取了某小学同年级部分学生进行跳绳测试，将所得数据整理后，画出频率分布直方图如图所示，已知图中从左到右前三个小组的频率分别是0.1，0.3，0.4，第一小组的频数为5.
（1）求第四小组的频率；
（2）参加这次测试的学生人数是多少？
（3）在这次测试中，学生跳绳次数的中位数落在第几小组内？
等比数列{
}的前n 项和为
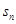，已知
,
,
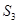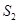成等差数列.
（Ⅰ）求{}的公比q；
（Ⅱ）求
－
＝3，求数列{}的通项公式
（Ⅲ）数列{n}的前n项的和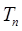
已知函数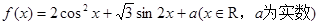
．
（Ⅰ）求f（x）的周期和单调递增区间；
（Ⅱ）若x∈[0，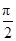
]时，f（x）的最大值为4，求a的值，并指出这时x的值．
工厂用两种原料A、B配成甲、乙两种药品，每生产一箱甲药品使用4kg的A原料，耗时1小时，每生产一箱乙药品使用4kg的B原料，耗时2小时，该厂每天最多可从原料厂获取16kg的A原料和12kg的B原料，每天只能有8小时的合成生产时间，该厂生产一箱甲药品获得3万元，生产一箱乙药品获得1万元，怎样安排生产才能获利最大？最大利润是多少？
用
长的金属条做一个“日”字型的窗户，当窗户的长和宽各为多少的时，透过的光线最多？
设不等式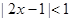
的解集是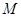
，
．
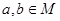（I）试比较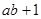
与
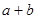的大小；
（II）设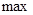
表示数集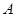
的最大数．
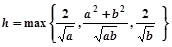,求证：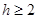
．