已知抛物线 与双曲线
与双曲线 有公共焦点
有公共焦点 ,点
,点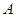 是曲线
是曲线 在第一象限的交点,且
在第一象限的交点,且 .
.
(1)求双曲线 的方程;
的方程;
(2)以双曲线 的另一焦点
的另一焦点 为圆心的圆
为圆心的圆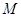 与直线
与直线 相切,圆
相切,圆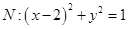 .过点
.过点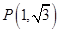 作互相垂直且分别与圆
作互相垂直且分别与圆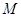 、圆
、圆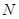 相交的直线
相交的直线 和
和 ,设
,设 被圆
被圆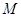 截得的弦长为
截得的弦长为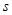 ,
, 被圆
被圆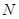 截得的弦长为
截得的弦长为 ,问:
,问: 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
(本小题满分12分)
已知函数f(x)="lnx-ax-3" (a≠0).
(1)讨论函数f(x)的单调性;
(2)若对于任意的a∈[1,2],函数g(x)=x3+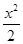 [m-2f′(x)]在区间(a,3)上有最值,求实数m的取值范围
[m-2f′(x)]在区间(a,3)上有最值,求实数m的取值范围
已知向量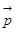 =(sinA,cosA),
=(sinA,cosA),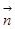 =(cosB,sinB),且
=(cosB,sinB),且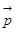 ·
·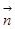 =sin2C,其中A,B,C分别为△ABC的三边a,b,c所对的角.
=sin2C,其中A,B,C分别为△ABC的三边a,b,c所对的角.
(1)求角C的大小;
(2)已知A=75°,c=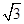 (cm),求△ABC的面积
(cm),求△ABC的面积
选修4-5:不等式选讲
已知函数 .
.
(Ⅰ)当a=3时,求函数 的最大值;
的最大值;
(Ⅱ)解关于x的不等式
选修4-4:坐标系与参数方程
在直角坐标系xOy中,直线 的参数方程为
的参数方程为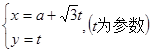 .在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
.在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 .
.
(Ⅰ)求圆C在直角坐标系中的方程;
(Ⅱ)若圆C与直线 相切,求实数a的值.
相切,求实数a的值.
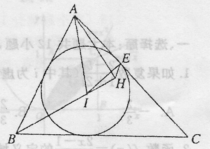
如图,锐角△ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为内切圆I与边CA的切点.
(Ⅰ)求证:四点A,I,H,E共圆;
(Ⅱ)若∠C=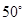 ,求∠IEH的度数.
,求∠IEH的度数.