【原创】（本小题满分13分）已知函数
，其中
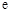为自然对数的底数．
（Ⅰ）求曲线
在点
处的切线方程；
（Ⅱ）若对任意
，不等式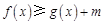
恒成立，求实数
的取值范围；
（Ⅲ）试探究当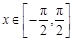
时，方程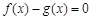
解的个数，并说明理由．
已知
矩阵
对应的线性变换把点
变成点
，求矩阵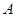
的特征值以及属于没个特征值的一个特征向量.
已知函数
（
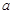为实常数）。
（Ⅰ）当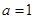
时，求函数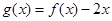
的单调区间；
（Ⅱ）若函数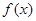
在区间
上无极值，求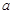的取值范围；
（Ⅲ）已知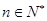
且
，求证: 
.
已知A、B、C是椭圆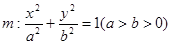
上的三点，其中点A的坐标为
，BC过椭圆m的中心，且
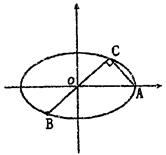
（1）求椭圆
的方程；
（2）过点
的直线l（斜率存在时）与椭圆m交于两点P，Q，
设D为椭圆m与y轴负半轴的交点，且
，求实数t的取值范围．
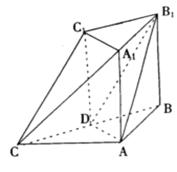
如图：在多面体
中，
，
,
，
。
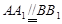（1）求证：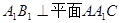
;
(2)求证：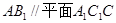
；
（3）求二面角
的余弦值。
设数列
的前项和为
，且
，
为等差数列，且
，
(Ⅰ)求数列和通项公式；
(Ⅱ)设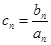
，求数列
的前
项和
．