(本小题满分12分）
已知直线l1:4x:-3y+6=0和直线l2x=-p/2:.若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.
(I )求抛物线C的方程；
(II)若以拋物线上任意一点M为切点的直线l与直线l2交于点N，试问在x轴上是否存 在定点Q，使Q点在以MN为直径的圆上，若存在，求出点Q的坐标，若不存在，请说明理由.
已知函数f(x),当x,y∈R时，恒有f(x+y)=f(x)+f(y).
(1)求证：f(x)是奇函数；
（2）如果x∈R+，f（x）＜0,并且f(1)=-
,试求f(x)在区间［-2，6］上的最值.
判断下列函数的奇偶性.
（1）f(x)=
;
(2)f(x)=log2(x+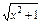
) (x∈R);
(3)f(x)=lg|x-2|.
已知f(x)=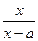
(x≠a).
（1）若a=-2,试证f(x)在（-∞,-2）内单调递增；
（2）若a＞0且f(x)在（1,+∞）内单调递减，求a的取值范围.
函数f(x)对任意的实数m、n有f(m+n)=f(m)+f(n),且当x＞0时有f(x)＞0.
（1）求证：f(x)在（-∞,+∞)上为增函数；
（2）若f(1)=1,解不等式f［log2(x2-x-2)］＜2.
已知f(x)在定义域（0，+∞）上为增函数，且满足f(xy)=f(x)+f(y),f(3)=1,试解不等式f(x)+f(x-8)≤2.