某次的一次学科测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
(1)求参加测试的总人数及分数在[80,90)之间的人数;
(2)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,恰有一份分数在[90,100)之间的概率.
(本小题满分14分)如图,四棱锥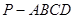 的底面
的底面 为正方形,
为正方形,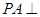 底面
底面 ,
,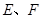 分别是
分别是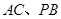 的中点.
的中点.
(1)求证: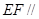 平面
平面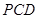 ;
;
(2)求证:平面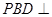 平面
平面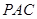 .
.
(本小题满分14分)设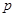 :实数
:实数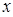 满足
满足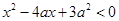 ,其中
,其中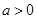 ,
, 实数
实数 满足
满足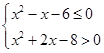
(1)若 ,且p∧q为真,求实数
,且p∧q为真,求实数 的取值范围.
的取值范围.
(2)﹁p是﹁q的充分不必要条件,求实数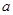 的取值范围.
的取值范围.
(本小题满分12分)设 上的两点,已知向量
上的两点,已知向量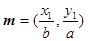 ,
,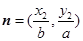 ,若
,若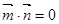 且椭圆的离心率
且椭圆的离心率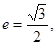 短轴长为2,
短轴长为2,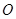 为 坐标原点.
为 坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线 过椭圆的焦点
过椭圆的焦点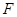 (0,c),(c为半焦距),求直线
(0,c),(c为半焦距),求直线 的斜率
的斜率 的值;
的值;
(Ⅲ)试问: 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
(本小题满分12分)(理科做)如图,四棱锥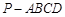 的底面
的底面 是直角梯形,
是直角梯形,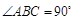 ,
, ,且
,且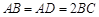 ,顶点
,顶点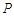 在底面
在底面 内的射影恰好落在
内的射影恰好落在 的中点
的中点 上.
上.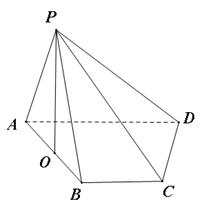
(1)求证: ;
;
(2)若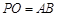 ,求直线
,求直线 与
与 所成角的 余弦值;
所成角的 余弦值;
(3)若平面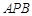 与平面
与平面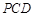 所成的二面角为
所成的二面角为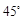 ,求
,求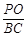 的值.
的值.
(文科做)设函数 .
.
(1)当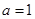 时,试求函数
时,试求函数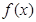 在区间
在区间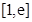 上的最大值;
上的最大值;
(2)当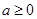 时,试求函数
时,试求函数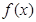 的单调区间.
的单调区间.
(本小题满分12分)甲乙两人各有 个材质、大小、形状完全相同的小球,甲的小球上面标有
个材质、大小、形状完全相同的小球,甲的小球上面标有 五个数字,乙的小球上面标有
五个数字,乙的小球上面标有 五个数字.把各自的小球放入两个不透明的口袋中,两人同时从各自的口袋中随机摸出
五个数字.把各自的小球放入两个不透明的口袋中,两人同时从各自的口袋中随机摸出 个小球.规定:若甲摸出的小球上的数字是乙摸出的小球上的数字的整数倍,则甲获胜,否则乙获胜.
个小球.规定:若甲摸出的小球上的数字是乙摸出的小球上的数字的整数倍,则甲获胜,否则乙获胜.
(1)写出基本事件空间 ;
;
(2)你认为“规定”对甲、乙二人公平吗?说出你的理由.