(本小题满分12分)
如图,已知三棱柱ABC-A1B1C1,侧面BCC1B1丄底面ABC.
(I)若M、N分别是AB,A1C的中点,求证:MN//平面BCC1B1
(II)若三棱柱ABC-A1B1C1的各棱长均为2,侧棱BB1与底面 ABC所成的角为60°.问在线段A1C1上是否存在一点P,使得平面B1CP丄平面ACC1A1,若存在,求C1P与PA1的比值,若不存在,说明 理由.
(本小题满分13分)
已知函数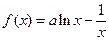 ,
,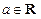 .
.
(Ⅰ)若曲线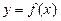 在点
在点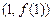 处的切线与直线
处的切线与直线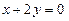 垂直,求
垂直,求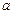 的值;
的值;
(Ⅱ)求函数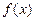 的单调区间;
的单调区间;
(Ⅲ)当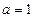 ,且
,且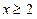 时,证明:
时,证明: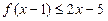 .
.
(本小题满分13分)
已知椭圆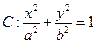
 的离心率为
的离心率为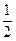 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线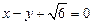 相切.
相切.
(Ⅰ)求椭圆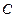 的方程;
的方程;
(Ⅱ)设 ,
,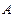 ,
,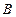 是椭圆
是椭圆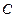 上关于
上关于 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆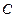 于另一点
于另一点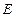 ,证明直线
,证明直线 与
与 轴相交于定点
轴相交于定点 ;
;
(Ⅲ)在(Ⅱ)的条件下,过点 的直线与椭圆
的直线与椭圆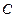 交于
交于 ,
,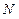 两点,求
两点,求 的取值范围.
的取值范围.
已知函数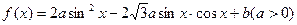 的定义域为
的定义域为 ,值域为
,值域为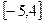 。试求函数
。试求函数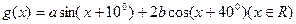
 的最小正周期T和最值。
的最小正周期T和最值。
已知函数
(1)设 为何值时,函数y取得最小值;
为何值时,函数y取得最小值;
(2)若函数y的最小值为1,试求a的值.
已知函数 ,
,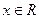 .求:
.求:
(Ⅰ) 函数
函数 的最大值及取得最大值的自变量
的最大值及取得最大值的自变量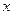 的集合;
的集合;
(II)函数 的单调增区间.
的单调增区间.