(本小题满分13分)
已知椭圆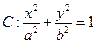
 的离心率为
的离心率为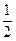 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线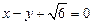 相切.
相切.
(Ⅰ)求椭圆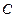 的方程;
的方程;
(Ⅱ)设 ,
,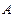 ,
,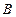 是椭圆
是椭圆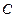 上关于
上关于 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆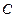 于另一点
于另一点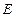 ,证明直线
,证明直线 与
与 轴相交于定点
轴相交于定点 ;
;
(Ⅲ)在(Ⅱ)的条件下,过点 的直线与椭圆
的直线与椭圆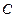 交于
交于 ,
,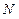 两点,求
两点,求 的取值范围.
的取值范围.
某高校在2011年的自主招生考试成绩中随机抽取 100名学生的笔试成绩,按成绩分组,得到的频率分布表如下所示.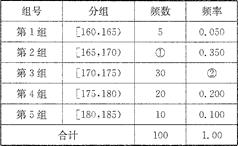

(1)请先求出频率分布表中①,②位置相应的数据,再完成下列频率分布直方图;并确定中位数。(结果保留2位小数)
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的条件下,学校决定在6名学生中随机抽取2名学生接受考官进行面试,求第4组至少有一名学生被考官A面试的概率?
如图所示,已知正方形 和矩形
和矩形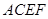 所在的平面互相垂直,
所在的平面互相垂直,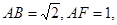
 是线段
是线段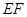 的中点。
的中点。
(1)证明: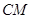 ∥平面
∥平面
(2)求异面直线 与
与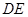 所成的角的余弦值。
所成的角的余弦值。
一个口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
(Ⅰ)求甲赢且编号的和为6的事件发生的概率;
(Ⅱ)这种游戏规则公平吗?试用概率说明理由.
如图,已知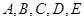 均在⊙O上,且
均在⊙O上,且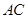 为⊙O的直径。
为⊙O的直径。
(1)求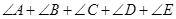 的值;
的值;
(2)若⊙O的半径为 ,
, 与
与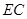 交于点
交于点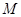 ,且
,且 、
、 为弧
为弧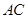 的三等分点,求
的三等分点,求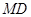 的长.
的长.
已知函数 ,
,
(Ⅰ)若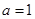 ,求函数
,求函数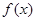 的极值;
的极值;
(Ⅱ)设函数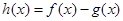 ,求函数
,求函数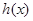 的单调区间;
的单调区间;
(Ⅲ)若在区间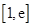 (
(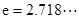 )上存在一点
)上存在一点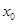 ,使得
,使得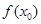
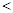
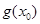 成立,求
成立,求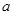 的取值范围.
的取值范围.