在△ABC中,内角A,B,C的对边分别为a,b,c,若b=1,c= .
.
(Ⅰ)求角C的取值范围;
(Ⅱ)求4sinCcos(C )的最小值.
)的最小值.
(本小题满分13分)
已知函数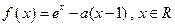 .
.
(1)若实数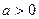 ,求函数
,求函数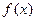 在
在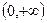 上的极值;
上的极值;
(2)记函数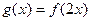 ,设函数
,设函数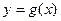 的图象C与
的图象C与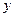 轴交于
轴交于 点,曲线C在
点,曲线C在 点处的切线与两坐标轴所围成的图形的面积为
点处的切线与两坐标轴所围成的图形的面积为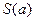 ,求当
,求当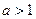 时
时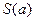 的最小值。
的最小值。
(本小题满分12分)
已知四边形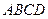 是边长为
是边长为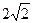 的正方形,
的正方形,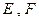 分别为
分别为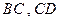 的中点,沿
的中点,沿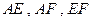 将
将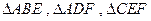 向同侧折叠且与平面
向同侧折叠且与平面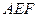 成直二面角,连接
成直二面角,连接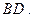
(1)求证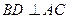 ;
;
(2)求平面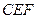 与平面
与平面 所成锐角的余弦值。
所成锐角的余弦值。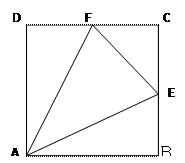

(本小题满分12分)
上海世博会于2010年5月1日正式开幕,按规定个人参观各场馆需预约,即进入园区后持门票当天预约,且一张门票每天最多预约六个场馆。考虑到实际情况(排队等待时间等),张华决定参观甲、乙、丙、丁四个场馆。假设甲、乙、丙、丁四个场馆预约成功的概率分别是 且它们相互独立互不影响。
且它们相互独立互不影响。
(1)求张华能成功预约甲、乙、丙、丁中两个场馆的概率;
(2)用 表示能成功预约场馆的个数,求随机变量
表示能成功预约场馆的个数,求随机变量 的分布列和数学期望。
的分布列和数学期望。
(本小题满分12分)
已知 函数
函数

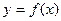 的图象的相邻两对称轴之间距离为2,且过点
的图象的相邻两对称轴之间距离为2,且过点
(1)求 的表达式;
的表达式;
(2)求 的单调递增区间。
的单调递增区间。
(本题满分 13分)
集合 为集合
为集合 的
的 个不同的子集,对于任意不大于
个不同的子集,对于任意不大于 的正整数
的正整数 满足下列条件:
满足下列条件:
① ,且每一个
,且每一个 至
至 少含有三个元素;
少含有三个元素;
②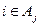 的充要条件是
的充要条件是 (其中
(其中 )。
)。
为了表示这些子集,作 行
行 列的数表(即
列的数表(即 数表),规定第
数表),规定第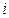 行第
行第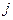 列数为:
列数为: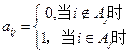 。
。
(1)该表中每一列至少有多少个1;若集合 ,请完成下面
,请完成下面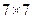 数表(填符合题意的一种即可);
数表(填符合题意的一种即可);
(2)用含 的代数式表示
的代数式表示 数表
数表 中1的个数
中1的个数 ,并证明
,并证明 ;
;
(3)设数列 前
前 项和为
项和为 ,数列
,数列 的通项公式为:
的通项公式为: ,证明不等式:
,证明不等式: 对任何正整数
对任何正整数 都成立。
都成立。