⊙O1和⊙O2的极坐标方程分别为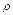 =4cos
=4cos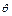 ,
,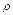 =-4sin
=-4sin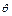 .
.
(1)把⊙O1和⊙O2的极坐标方程化为直角坐标方程;
(2)求经过⊙O1,⊙O2交点的直线的直角坐标方程.
已知函数 ,
, .
.
(1)若直线 是函数
是函数 的图像的一条对称轴,求
的图像的一条对称轴,求 的值;
的值;
(2)若 ,求
,求 的值域.
的值域.
已知函数 (
( ).
).
(Ⅰ)当 时,求函数
时,求函数 的图象在点
的图象在点 处的切线方程;
处的切线方程;
(Ⅱ)当 时,记函数
时,记函数 ,试求
,试求 的单调递减区间;
的单调递减区间;
(Ⅲ)设函数 (其中
(其中 为常数),若函数
为常数),若函数 在区间
在区间 上不存在极值,求
上不存在极值,求 的最大值.
的最大值.
已知抛物线
 的焦点为
的焦点为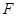 ,抛物线上存在一点
,抛物线上存在一点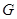 到焦点的距离为
到焦点的距离为 ,且点
,且点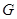 在圆
在圆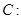
 上.
上.
(Ⅰ)求抛物线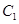 的方程;
的方程;
(Ⅱ)已知椭圆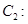
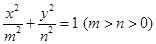 的一个焦点与抛物线
的一个焦点与抛物线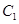 的焦点重合,且离心率为
的焦点重合,且离心率为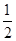 .直线
.直线 交椭圆
交椭圆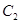 于
于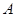 、
、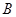 两个不同的点,若原点
两个不同的点,若原点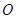 在以线段
在以线段 为直径的圆的外部,求
为直径的圆的外部,求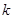 的取值范围.
的取值范围.
如图,在正四棱台 中,
中, ,
,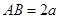 ,
, ,
, 、
、 分别是
分别是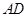 、
、 的中点.
的中点. 
(Ⅰ)求证:平面 ∥平面
∥平面 ;
;
(Ⅱ)求证: 平面
平面 .
.
注:底面为正方形,从顶点向底面作垂线,垂足是底面中心,这样的四棱锥叫做正四棱锥.用一个平行于正四棱锥底面的平面去截该棱锥,底面与截面之间的部分叫做正四棱台.
已知向量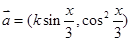 ,
,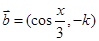 ,实数
,实数 为大于零的常数,函数
为大于零的常数,函数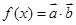 ,
, ,且函数
,且函数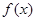 的最大值为
的最大值为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)在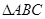 中,
中, 分别为内角
分别为内角 所对的边,若
所对的边,若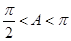 ,
, ,且
,且 ,
, ,求
,求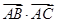 的值.
的值.