已知抛物线
 的焦点为
的焦点为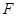 ,抛物线上存在一点
,抛物线上存在一点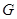 到焦点的距离为
到焦点的距离为 ,且点
,且点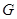 在圆
在圆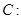
 上.
上.
(Ⅰ)求抛物线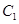 的方程;
的方程;
(Ⅱ)已知椭圆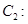
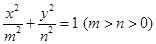 的一个焦点与抛物线
的一个焦点与抛物线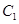 的焦点重合,且离心率为
的焦点重合,且离心率为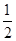 .直线
.直线 交椭圆
交椭圆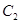 于
于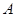 、
、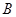 两个不同的点,若原点
两个不同的点,若原点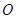 在以线段
在以线段 为直径的圆的外部,求
为直径的圆的外部,求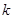 的取值范围.
的取值范围.
已知数列 中,
中, ,且
,且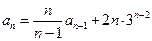
 .
.
(Ⅰ) 求数列 的通项公式;
的通项公式;
(Ⅱ) 令
 ,数列
,数列 的前
的前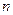 项和为
项和为 ,试比较
,试比较 与
与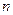 的大小;
的大小;
(Ⅲ) 令
 ,数列
,数列 的前
的前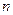 项和为
项和为 .求证:对任意
.求证:对任意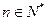 ,
,
都有 .
.
已知函数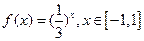 ,函数
,函数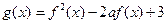 的最小值为
的最小值为 .
.
(1)求 的解析式;
的解析式;
(2)是否存在实数 同时满足下列两个条件:①
同时满足下列两个条件:① ;②当
;②当 的定义域为
的定义域为 时,值域为
时,值域为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知二次函数 ,不等式
,不等式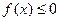 的解集有且只有一个元素,设数列
的解集有且只有一个元素,设数列 的前
的前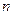 项和为
项和为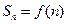 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设各项均不为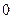 的数列
的数列 中,满足
中,满足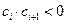 的正整数
的正整数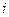 的个数称作数列
的个数称作数列 的变号数,令
的变号数,令 ,求数列
,求数列 的变号数.
的变号数.
已知 中,
中,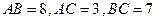 ,
, 为圆心,直径
为圆心,直径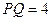 ,求
,求 的最大值、最小值,并分别指出取得最值时
的最大值、最小值,并分别指出取得最值时 与
与 夹角的大小.
夹角的大小.
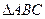
 中,角
中,角 的对边分别为
的对边分别为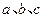 ,且
,且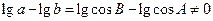 .
.
(1)判断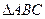 的形状;
的形状;
(2)设向量 ,
, ,且
,且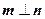 ,
, ,求
,求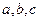 .
.