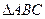
 中,角
中,角 的对边分别为
的对边分别为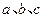 ,且
,且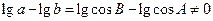 .
.
(1)判断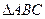 的形状;
的形状;
(2)设向量 ,
, ,且
,且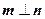 ,
, ,求
,求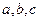 .
.
已知函数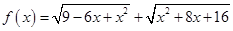
⑴解不等式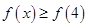 ;
;
⑵设函数 ,若不等式
,若不等式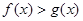 恒成立,求实数
恒成立,求实数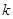 的取值范围.
的取值范围.
已知曲线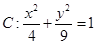 ,直线
,直线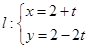 (t为参数).
(t为参数).
(1)写出曲线C的参数方程,直线 的普通方程;
的普通方程;
(2)过曲线C上任意一点P作与 夹角为30°的直线,交
夹角为30°的直线,交 于点A,求|PA|的最大值与最小值.
于点A,求|PA|的最大值与最小值.
如图,圆周角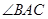 的平分线与圆交于点
的平分线与圆交于点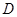 ,过点
,过点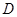 的切线与弦
的切线与弦 的延长线交于点
的延长线交于点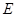 ,
,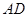 交
交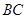 于点
于点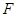 .
.
(1)求证: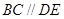 ;
;
(2)若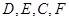 四点共圆,且弧
四点共圆,且弧 与弧
与弧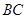 相等,求
相等,求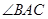 .
.
已知函数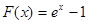 ,
,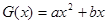 ,其中
,其中 ,
,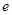 是自然对数的底数.
是自然对数的底数.
(1)当 时,
时,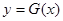 为曲线
为曲线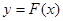 的切线,求
的切线,求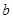 的值;
的值;
(2)若 ,
, ,且函数
,且函数 在区间
在区间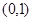 内有零点,求实数
内有零点,求实数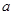 的取值范围.
的取值范围.
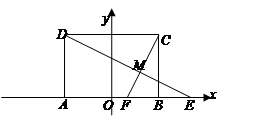
在矩形中 中,
中,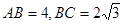 ,
, 为动点,
为动点,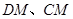 的延长线与
的延长线与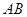 (或其延长线)分别交于点
(或其延长线)分别交于点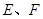 ,若
,若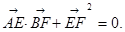
(1)若以线段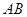 所在的直线为
所在的直线为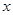 轴,线段
轴,线段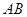 的中垂线为
的中垂线为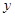 轴建立平面直角坐标系,试求动点
轴建立平面直角坐标系,试求动点 的轨迹方程;
的轨迹方程;
(2)不过原点的直线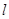 与(1)中轨迹交于
与(1)中轨迹交于 两点,若
两点,若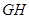 的中点
的中点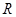 在抛物线
在抛物线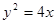 上,求直线
上,求直线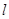 的斜率
的斜率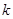 的取值范围.
的取值范围.