某校100名学生期中考试语文成绩的频率分布直方图如图所示，其-优题课

题文

某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50,60），[60,70），[70,80），[80,90），[90,100]．

（1）求图中a的值；
（2）根据频率分布直方图，估计这100名学生语文成绩的平均分；
（3）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如下表所示，
求数学成绩在[50,90）之外的人数．

分数段	[50,60）	[60, 70）	[70,80）	[80,90）
x∶y	1∶1	2∶1	3∶4	4∶5

科目数学题型解答题难度中等

知识点：误差估计

登录免费查看答案和解析

相关试题

（本小题满分12分）如图，在空间四边形PABC中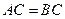，，，．求证：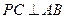

（本小题满分10分）已知边长为6的正方形ABCD所在平面外一点P，PD^平面ABCD，PD=8，求PB与平面ABCD所成的角的大小；

已知数列 $\{a_{n}\}$ 和 $\{b_{n}\}$ 满足： $a_{1} = λ$ ， $a_{n + 1} = \frac{2}{3} a_{n} + n - 4$ ， $b_{n} = (- 1)^{n} (a_{n} - 3 n + 21)$ ，其中 $λ$ 为实数， $n$ 为正整数。

（Ⅰ）证明：对任意的实数 $λ$ ，数列 $\{a_{n}\}$ 不是等比数列；

（Ⅱ）设 $S_{n}$ 为数列 $\{b_{n}\}$ 的前 $n$ 项和，是否存在实数 $λ$ ，使得对任意正整数 $n$ ，都有 $S_{n} > - 12$ ?若存在，求 $λ$ 的取值范围；若不存在，说明理由.

已知双曲线 $C : \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)$ 的两个焦点为 $F : (- 2, 0), F : (2, 0)$ $点 P (3, \sqrt{7})$ 的曲线 $C$ 上.
（Ⅰ）求双曲线 $C$ 的方程；
（Ⅱ）记 $O$ 为坐标原点，过点 $Q (0, 2)$ 的直线 $l$ 与双曲线 $C$ 相交于不同的两点 $E, F$ ，若 $△ O E F$ 的面积为 $2 \sqrt{2}$ 求直线 $l$ 的方程

如图，要设计一张矩形广告，该广告含有大小相等的左右两个矩形栏目（即图中阴影部分），这两栏的面积之和为18000cm ^2,四周空白的宽度为10cm，两栏之间的中缝空白的宽度为5cm，怎样确定广告的高与宽的尺寸（单位：cm），能使矩形广告面积最小？

试卷网试题网古诗词网作文网范文网

Copyright ©2020-2025 优题课 youtike.com 版权所有

粤ICP备20024846号