已知a>0,设命题p:函数y=ax在R上单调递减,q:不等式x+|x-2a|>1的解集为R,若p和q中有且只有一个命题为真命题,求a的取值范围.
已知函数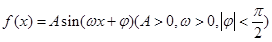 ,的部分图象如图所示.
,的部分图象如图所示.
(1) 求函数 的解析式;
的解析式;
(2) 如何由函数
 的图象通过适当的平移与伸缩变换得到函数
的图象通过适当的平移与伸缩变换得到函数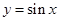 的图象,写出变换过程.
的图象,写出变换过程.
已知奇函数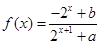 是定义域为
是定义域为 的减函数
的减函数
(Ⅰ)求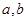 的值;
的值;
(Ⅱ)若对任意的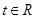 ,不等式
,不等式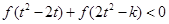 恒成立,求
恒成立,求 的取值范围;
的取值范围;
已知三角形 的顶点坐标为
的顶点坐标为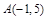 ,
,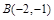 ,
,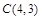 ,
,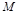 是
是 边上的中点。
边上的中点。
(Ⅰ)求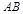 边所在直线的方程;
边所在直线的方程;
(Ⅱ)求中线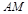 的长;
的长;
(Ⅲ)求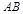 边的高所在直线的方程。
边的高所在直线的方程。
如图,已知在侧棱垂直于底面三棱柱ABC—A1B1C1中,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.
(Ⅰ)求证:AC⊥BC1;
(Ⅱ)求证:AC1∥平面CDB1.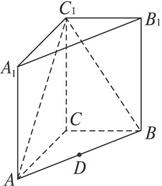
已知直线l经过点P(-2,5),且斜率为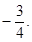
(Ⅰ)求直线l的方程;
(Ⅱ)若直线m与l平行,且点P到直线m的距离为3,求直线m的方程.