某工厂对200个电子元件的使用寿命进行检查,按照使用寿命(单位:h),可以把这批电子元件分成第一组[100,200],第二组(200,300],第三组(300,400],第四组(400,500],第五组(500,600],第六组(600,700].由于工作中不慎将部分数据丢失,现有以下部分图表: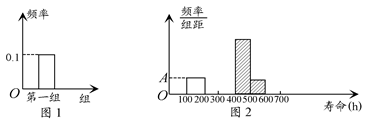
| 分组 |
[100,200] |
(200,300] |
(300,400] |
(400,500] |
(500,600] |
(600,700] |
| 频数 |
B |
30 |
E |
F |
20 |
H |
| 频率 |
C |
D |
0.2 |
0.4 |
G |
I |
(1)求图2中的A及表格中的B,C,D,E,F,G,H,I的值;
(2)求图2中阴影部分的面积;
(3)若电子元件的使用时间超过300h为合格产品,求这批电子元件合格的概率.
、(本小题满分12分)
在三棱锥 中,
中, 是边长为
是边长为 的正三角形,平面
的正三角形,平面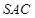 ⊥平面
⊥平面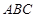 ,
, ,
, 、
、 分别为
分别为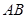 、
、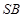 的中点。
的中点。
(1)证明: ⊥
⊥ ;
;
(2)求三棱锥 的体积.
的体积.
(本小题满分12分)
已知 的面积为
的面积为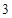 ,且满足
,且满足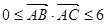 ,设
,设 和
和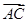 的夹角为
的夹角为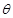
(I)求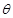 的取值范围;(II)求函数
的取值范围;(II)求函数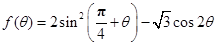 的最大值与最小值
的最大值与最小值
已知函数f(x)= |x-1|,g(x)=" -" |x+3| + a (aÎR)
(1)解关于 的不等式
的不等式 ;
;
(2)若函数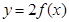 的图像恒在函数
的图像恒在函数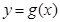 的图像的上方,求实数
的图像的上方,求实数 的取值范围.
的取值范围.
.已知直线 的参数方程是
的参数方程是 (t是参数)圆C的极坐标方程为
(t是参数)圆C的极坐标方程为 .
.
(1)求圆C在直角坐标系下的方程;
(2)由直线 上的点向圆引切线,求切线长的最小值.
上的点向圆引切线,求切线长的最小值.
A 为圆外一点,AB,AC分别交圆于D, E, AB, AC的长分别是一元二次方程x2-x+(m2 –m +  )=0
)=0
的两个根.( 如图所示)(1)求m的值(2)求证:DE//BC