如图,直角三角形ABC的顶点A的坐标为(-2,0),直角顶点B的坐标为(0,-2),顶点C在x轴上.
(1)求BC边所在直线的方程.
(2)圆M是△ABC的外接圆,求圆M的方程.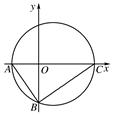
已知函数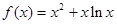
(Ⅰ)、求这个函数的导数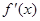
(Ⅱ)、求这个函数在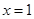 处的切线方程
处的切线方程
已知双曲线与椭圆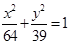 共焦点,且以
共焦点,且以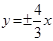 为渐近线,求双曲线的标准方程和离心率
为渐近线,求双曲线的标准方程和离心率
设命题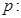 “方程
“方程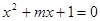 有两个实数根”,命题
有两个实数根”,命题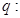 “方程
“方程 无实根”,若
无实根”,若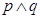 为假,
为假,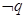 为假,求实数
为假,求实数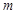 的取值范围.
的取值范围.
有粮食和石油两种物资,可用轮船与飞机两种方式运输,每天每艘轮船和每架飞机的运输效果见表.
 |
轮船运输量/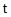 |
飞机运输量/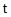 |
| 粮食 |
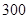 |
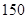 |
| 石油 |
 |
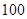 |
现在要在一天内运输至少 粮食和
粮食和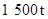 石油,需至少安排多少艘轮船和多少架飞机?
石油,需至少安排多少艘轮船和多少架飞机?
已知椭圆G的中心在坐标原点,长轴在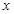 轴上,离心率为
轴上,离心率为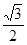 ,两个焦点分别为
,两个焦点分别为 和
和 ,椭圆G上一点到
,椭圆G上一点到 和
和 的距离之和为12.
的距离之和为12.
圆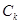 :
:
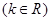 的圆心为点
的圆心为点 .
.
(1)求椭圆G的方程
(2)求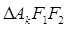 的面积
的面积
(3)问是否存在圆 包围椭圆G?请说明理由.
包围椭圆G?请说明理由.