写出下列命题的否定并判断真假.
(1)p:所有末位数字是0的整数都能被5整除;
(2)q: x≥0,x2>0;
x≥0,x2>0;
(3)r:存在一个三角形,它的内角和大于180°;
(4)t:某些梯形的对角线互相平分.
已知圆C经过 两点,且在
两点,且在 轴上截得的线段长为
轴上截得的线段长为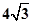 ,半径小于5.(1)求直线
,半径小于5.(1)求直线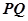 与圆C的方程;(2)若直线
与圆C的方程;(2)若直线 ,直线
,直线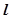 与圆C交于点A、B,且以AB为直径的圆经过坐标原点,求直线
与圆C交于点A、B,且以AB为直径的圆经过坐标原点,求直线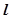 的方程.
的方程.
在△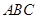 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为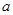 ,
, ,
,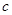 .
.
(1)若 ,求角
,求角 ;
;
(2)若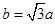 ,
,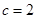 ,且△
,且△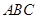 的面积为
的面积为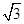 ,求
,求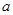 的值.
的值.
设向量a=(2,sinθ),b=(1,cosθ),θ为锐角(1)若a·b=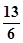 ,求sinθ+cosθ的值;(2)若a//b,求sin(2θ+
,求sinθ+cosθ的值;(2)若a//b,求sin(2θ+ )的值.
)的值.
已知函数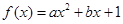 在
在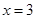 处的切线方程为
处的切线方程为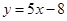 .
.
(1)求函数 的解析式;
的解析式;
(2)若关于 的方程
的方程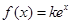 恰有两个不同的实根,求实数
恰有两个不同的实根,求实数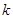 的值;
的值;
(3)数列 满足
满足 ,
, ,求
,求 的整数部分.
的整数部分.
已知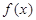 是定义在
是定义在 上的奇函数,当
上的奇函数,当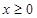 时,
时,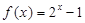 .
.
(1)求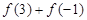 ;
;
(2)求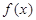 的解析式;
的解析式;
(3)若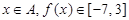 ,求区间
,求区间 .
.