已知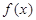 是定义在
是定义在 上的奇函数,当
上的奇函数,当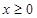 时,
时,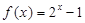 .
.
(1)求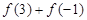 ;
;
(2)求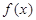 的解析式;
的解析式;
(3)若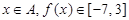 ,求区间
,求区间 .
.
已知函数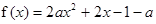 在区间
在区间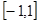 上有且只有一个零点,求实数
上有且只有一个零点,求实数 的取值范围。
的取值范围。
已知 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项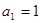 ,
, 的部分项
的部分项 、
、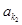 、 、
、 、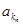 恰为等比数列,且
恰为等比数列,且 ,
, ,
, .
.
(1)求数列 的通项公式
的通项公式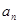 ;
;
(2)若数列 的前
的前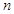 项和为
项和为 ,求
,求 .
.
如图,某单位准备修建一个面积为600平方米的矩形场地(图中 )的围墙,且要求中间用围墙
)的围墙,且要求中间用围墙 隔开,使得
隔开,使得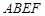 为矩形,
为矩形,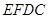 为正方形,设
为正方形,设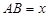 米,已知围墙(包括
米,已知围墙(包括 )的修建费用均为800元每米,设围墙(包括
)的修建费用均为800元每米,设围墙(包括 )的修建总费用为
)的修建总费用为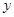 元。
元。
(1)求出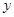 关于
关于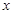 的函数解析式;
的函数解析式;
(2)当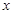 为何值时,设围墙(包括
为何值时,设围墙(包括 )的的修建总费用
)的的修建总费用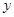 最小?并求出
最小?并求出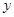 的最小值。
的最小值。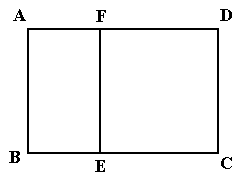
某校高三年级一次数学考试之后,为了解学生的数学学习情况, 随机抽取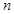 名学生的数学成绩, 制成下表所示的频率分布表.
名学生的数学成绩, 制成下表所示的频率分布表.
(1)求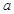 ,
,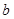 ,
,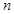 的值;
的值;
(2)若从第三, 四, 五组中用分层抽样方法抽取6名学生,并在这6名学生中随机抽取2名与张老师面谈,求第三组中至少有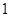 名学生与张老师面谈的概率.
名学生与张老师面谈的概率.
| 组号 |
分组 |
频数 |
频率 |
| 第一组 |
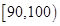 |
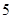 |
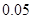 |
| 第二组 |
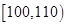 |
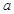 |
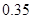 |
| 第三组 |
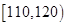 |
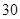 |
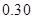 |
| 第四组 |
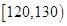 |
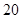 |
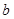 |
| 第五组 |
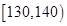 |
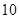 |
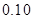 |
| 合计 |
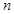 |
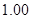 |
在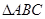 中,角
中,角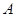 、
、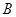 、
、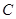 的对边分别为
的对边分别为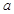 、
、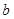 、
、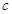 ,且
,且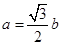 ,
,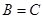 .(1) 求
.(1) 求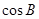 的值;
的值;
(2) 设函数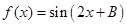 ,求
,求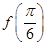 的值.
的值.